Choose the correct answer in questions 17 to 19:
If a, b, c are in A.P., then the determinant ⎡⎢⎣x+2x+3x+2ax+3x+4x+3bx+4x+5x+2c⎤⎥⎦ is :
(a) 0
(b) 1
( c) x
(d) 2xSolution in Gujrati
0
1
x
2x
The correct Answer is:A
Step by step video, text & image solution for Choose the correct answer in questions 17 to 19: If a, b, c are in A.P., then the determinant [{:(x+2,x+3,x+2a),(x+3,x+4,x+3b),(x+4,x+5,x+2c):}] is : (a) 0 (b) 1 ( c) x (d) 2x by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DETERMINANTS BOOK - NCERT GUJARATICHAPTER - DETERMINANTS EXERCISE - EXERCISE 4.6
16 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - NCERT GUJARATICHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER 5
23 Videos
- DIFFERENTIAL EQUATIONSBOOK - NCERT GUJARATICHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - MISCELLANEOUS EXERCISE
18 Videos
Similar Questions
Examine the consistency of the system of equationsx+2y=22x+3y=3
View SolutionDifferentiate w.r.t.x the function in Exercises 1 to 11.
(3x2−9x+5)9
View SolutionFor each of the differential equations given below, indicate its order and degree(if defined).
(i) d2ydx2+5x(dydx)2−6y=logx
(ii)(dydx)3−4(dydx)2+7y=sinx
(iii)d4ydx4−sin(d3ydx3=0
View Solution(A) in the above reaction ,maximum saytzeff product will obtained when : (a) X=-1 (b) X=-Cl(C ) X=-Br (D) X=-F (B) in the above reation Hoffmann product major when X is : (A) -I (b) -Cl(c ) -Br (D) -F
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View SolutionChoose the correct answer in questions 17 to 19:
If a, b, c are in A.P., then the determinant ⎡⎢⎣x+2x+3x+2ax+3x+4x+3bx+4x+5x+2c⎤⎥⎦ is :
(a) 0
(b) 1
( c) x
(d) 2x
View SolutionIf a, b,c are in A.P., then the value of the determinant ∣∣ ∣∣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c∣∣ ∣∣ is :
View SolutionIf a,b,c are A.P then the value of the determinant
∣∣ ∣∣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c∣∣ ∣∣
View SolutionIf a,b,c are in A.P. then the determinant
⎡⎢⎣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c⎤⎥⎦ is
View SolutionIf a,b,c are in A.P. then the determinant
∣(x+2,x+3,x+2a),(x+3,x+4,x+2b),(x+4,x+5,x+2c)|} is
View SolutionIf a,b,c are in A.P. then the determinant
∣(x+2,x+3,x+2a),(x+3,x+4,x+2b),(x+4,x+5,x+2c)|} is
View SolutionIf a,b,c are in A.P. then the determinant
⎡⎢⎣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c⎤⎥⎦ is
View SolutionIf a, b, c, are in A.P, then the determinant ∣∣ ∣∣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c∣∣ ∣∣ is
(A) 0 (B) 1 (C) x (D) 2x
View SolutionIf a, b, c, are in A.P, then the determinant∣∣ ∣∣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c∣∣ ∣∣is(A) 0 (B) 1 (C) x (D) 2x
View SolutionIf a,b,c are in A.P then the determinant
∣∣ ∣∣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c∣∣ ∣∣ is …..
View SolutionIf a,b,c are in A.P., then the determinant
∣∣ ∣∣x+2x+3x+2ax+3x+4x+2bx+4x+5x+2c∣∣ ∣∣ is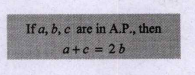
View Solution
