If the point inside a triangle are equidistant from the vertex of the same triangle, what the name of that point is ?
Incentre
Orthocentre
Median
Circumcentre
The correct Answer is:D
To solve the question, we need to identify the point inside a triangle that is equidistant from all three vertices of the triangle. Here's a step-by-step solution:
Step 1: Understand the Triangle and Points
We have a triangle, which we can label as triangle ABC. The vertices of the triangle are A, B, and C.
Hint: Visualize the triangle and label the vertices clearly.
Step 2: Define the Point Inside the Triangle
Let’s denote the point inside the triangle as point O. According to the problem, the distances from point O to each vertex of the triangle are equal. This means that OA = OB = OC.
Hint: Remember that the distances from point O to each vertex are crucial to identifying the type of point.
Step 3: Identify the Characteristics of Point O
Since point O is equidistant from all three vertices of triangle ABC, it satisfies a specific condition that is characteristic of a well-known point in triangle geometry.
Hint: Think about the special points in triangle geometry that relate to distances from vertices.
Step 4: Determine the Name of the Point
The point O, which is equidistant from the vertices A, B, and C, is known as the Circumcenter of the triangle. The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect, and it is equidistant from all three vertices.
Hint: Recall the definitions of various triangle centers (like centroid, orthocenter, and circumcenter) to confirm your answer.
Conclusion
The point inside the triangle that is equidistant from the vertices is called the Circumcenter.
---
We have a triangle, which we can label as triangle ABC. The vertices of the triangle are A, B, and C.
Let’s denote the point inside the triangle as point O. According to the problem, the distances from point O to each vertex of the triangle are equal. This means that OA = OB = OC.
Since point O is equidistant from all three vertices of triangle ABC, it satisfies a specific condition that is characteristic of a well-known point in triangle geometry.
The point O, which is equidistant from the vertices A, B, and C, is known as the Circumcenter of the triangle. The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect, and it is equidistant from all three vertices.
The point inside the triangle that is equidistant from the vertices is called the Circumcenter.
Similar Questions
Knowledge Check
A point P lying inside a triangle is equidistant from the vertices of the triangle. Then the triangle has P as its
ACentroidBIncentreCOrthocentreDCircumcentreThe equidistant point from the vertices of a triangle is called its :
ACentroidBIncentreCCircumcentreDOrthocentreThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
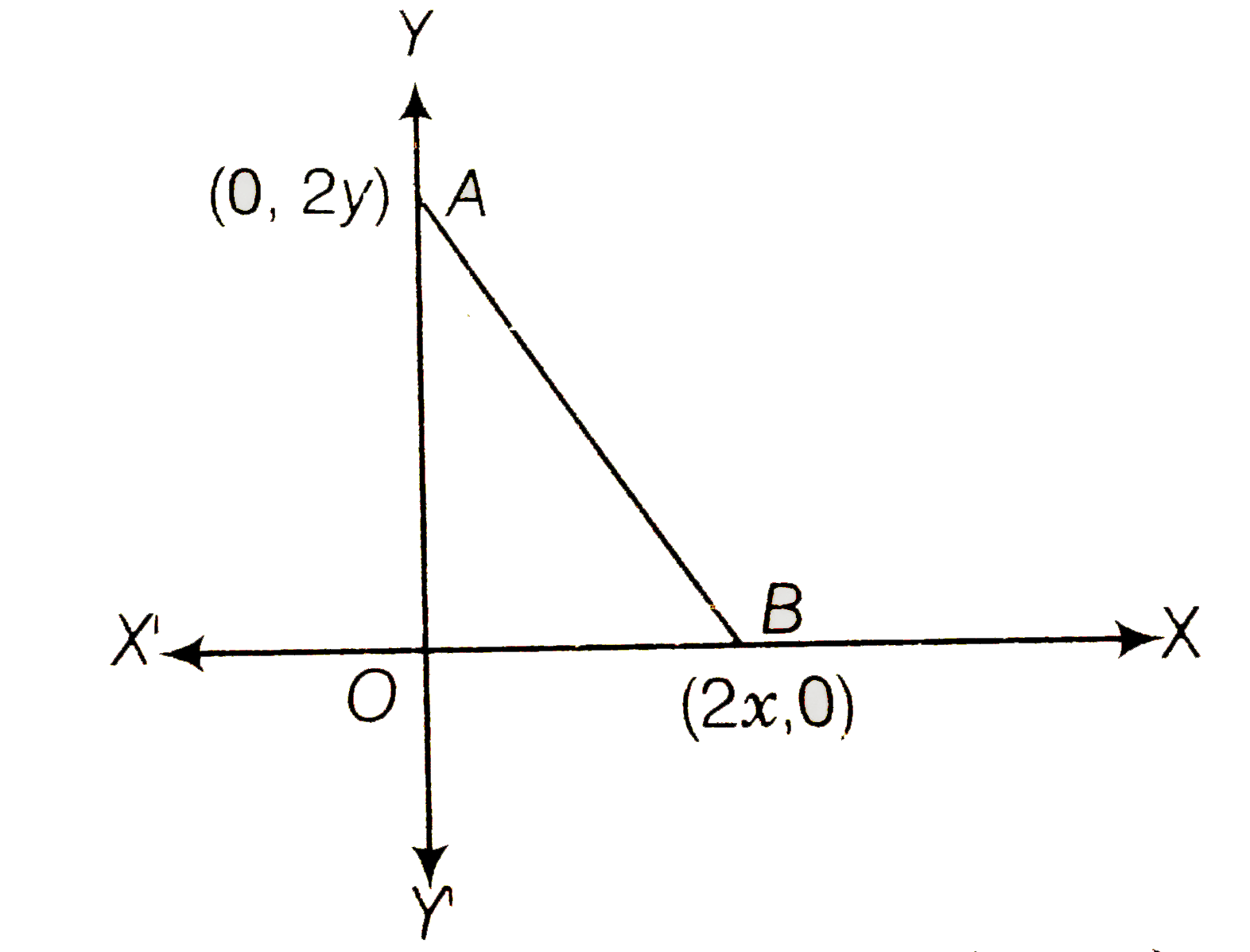 A(x,y)B(y,x)C(x2,y2)D(y2,x2)
A(x,y)B(y,x)C(x2,y2)D(y2,x2)
In an Isoceless triangle altitude from the vertex bisects the base.
View SolutionWhat is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
View SolutionProve by the vector method that the mid-point of the hypotenuse of a right angled triangleis equidistant from the vertices of the triangle.OR
View SolutionWhat is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
View SolutionThe locus of a point which is twice as far from each vertex of a triangle as it is from the mid-point of the opposite side is a/an/the _______
View Solution
