In each of the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series:
AZBY, ?, EVFU, GTHS
BYCZ
CXDR
CXDW
EXDZ
The correct Answer is:C
A+2−−→C+2−−→E+2−−→OZ−2−−→X−2−−→V−2−−→TB+2−−→D+2−−→F+2−−→HY−2−−→W−2−−→U−2−−→S
Similar Questions
In each of the following questions a series is given, with one term missing. Choose the correct alternatives from the given ones that will complete the series.
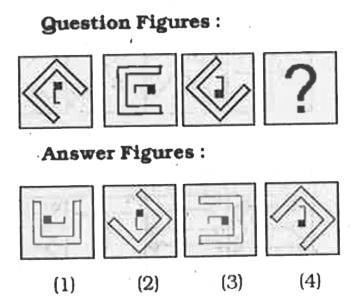
View SolutionIn each of the following questions a series is given, with one term missing. Choose the correct alternatives from the given ones that will complete the series.
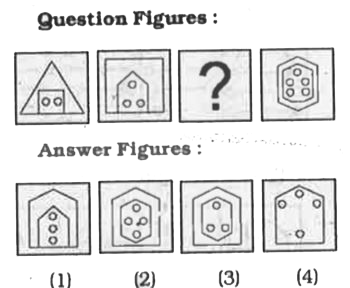
View Solution
Knowledge Check
In the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
AZBY, ?, EVFU, GTHSABYCZBCYDRCMISGDCXDWIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
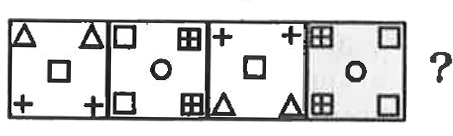 A
A B
B C
C D
D
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
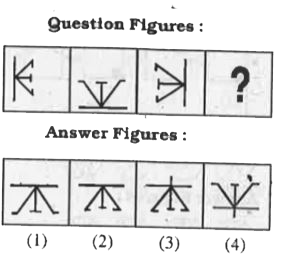
View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
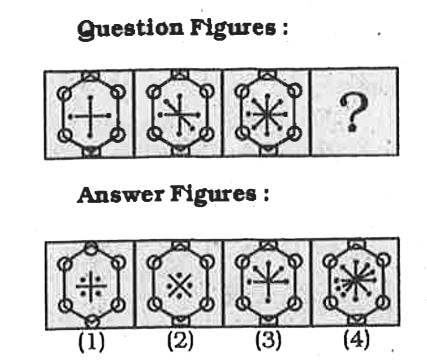
View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View Solution
