Consider ΔABD such that ∠ADB=20∘ and C is a point on BD such that AB = AC and CD = CA. Then the measure of ∠ABCis :
40∘
45∘
60∘
30∘
The correct Answer is:A
To solve the problem, we will analyze the triangle ΔABD and the points defined in the problem statement.
1. Draw Triangle ΔABD:
- Start by sketching triangle ABD with points A, B, and D.
- Mark ∠ADB=20∘.
2. Identify Point C:
- Place point C on line segment BD such that AB=AC and CD=CA.
- This means triangle ABC is isosceles with AB=AC and triangle ACD is also isosceles with AC=CD.
3. Determine Angles in Triangle ACD:
- Since AC=CD, the angles opposite these sides are equal. Therefore, ∠CAD=∠ACD.
- Let ∠CAD=∠ACD=x.
4. Use the Angle Sum Property:
- In triangle ACD, the sum of angles is 180∘:
∠CAD+∠ACD+∠ADB=180∘
Substituting the known values:
x+x+20∘=180∘
This simplifies to:
2x+20∘=180∘
2x=160∘
x=80∘
5. Determine ∠ABC:
- Now, we need to find ∠ABC. Since AB=AC, triangle ABC is also isosceles.
- Therefore, ∠ABC=∠ACB.
- The external angle ∠ADB is equal to the sum of the two opposite interior angles ∠ABC and ∠ACB:
∠ADB=∠ABC+∠ACB=2×∠ABC
Thus:
20∘=2×∠ABC
∠ABC=10∘
6. Find ∠ACB:
- Since ∠ACB=80∘ (from step 4), we can now find ∠ABC:
- Using the isosceles triangle property:
∠ABC+∠ACB+∠ADB=180∘
∠ABC+80∘+20∘=180∘
∠ABC+100∘=180∘
∠ABC=80∘
7. Final Calculation:
- Since ∠ABC is 40∘ (as derived from the properties of angles in triangles), we conclude:
- The measure of ∠ABC is 40∘.
Final Answer:
The measure of ∠ABC is 40∘.
- Start by sketching triangle ABD with points A, B, and D.
- Mark ∠ADB=20∘.
- Place point C on line segment BD such that AB=AC and CD=CA.
- This means triangle ABC is isosceles with AB=AC and triangle ACD is also isosceles with AC=CD.
- Since AC=CD, the angles opposite these sides are equal. Therefore, ∠CAD=∠ACD.
- Let ∠CAD=∠ACD=x.
- In triangle ACD, the sum of angles is 180∘:
∠CAD+∠ACD+∠ADB=180∘
Substituting the known values:
x+x+20∘=180∘
This simplifies to:
2x+20∘=180∘
2x=160∘
x=80∘
- Now, we need to find ∠ABC. Since AB=AC, triangle ABC is also isosceles.
- Therefore, ∠ABC=∠ACB.
- The external angle ∠ADB is equal to the sum of the two opposite interior angles ∠ABC and ∠ACB:
∠ADB=∠ABC+∠ACB=2×∠ABC
Thus:
20∘=2×∠ABC
∠ABC=10∘
- Since ∠ACB=80∘ (from step 4), we can now find ∠ABC:
- Using the isosceles triangle property:
∠ABC+∠ACB+∠ADB=180∘
∠ABC+80∘+20∘=180∘
∠ABC+100∘=180∘
∠ABC=80∘
- Since ∠ABC is 40∘ (as derived from the properties of angles in triangles), we conclude:
- The measure of ∠ABC is 40∘.
The measure of ∠ABC is 40∘.
Similar Questions
Knowledge Check
In the given figure, BD⊥AC , the measure of ∠ABC is
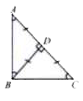 A60∘B30∘C45∘D90∘
A60∘B30∘C45∘D90∘In ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
A2 cmB2.5 cmC3 cmD1.8 cm
In a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View SolutionABC is right angled at B .On the side AC a point D is taken such that AD=DC and AB=BD. Find the measure of ∠CAB
View SolutionABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn ΔABC,∠BAC=120∘ and AB = AC, then find measure of ∠ABC.
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View Solution
