A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50Nm−1. The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.Solution in Bengali
The block executes SHM, its angular frequency, as given by Eq. (14.14b), is
ω=√km
=√50Nm−11kg
=7.07rads−1
Its displacement at any time t is then given by,
x(t) = 0.1 cos (7.07t)
Therefore, when the particle is 5 cm away from the mean position, we have
0.05 = 0.1 cos (7.07t)
Or cos (7.07t) = 0.5 and hence
sin(7.07t)=√32=0.866
Then, the velocity of the block at x = 5 cm is
=0.1×7.07×0.866ms−1
=0.61ms−1
Hence the K.E. of the block,
=12mv2
=12[1kg×(0.6123ms−1)2]
=0.19J
The P.E. of the block,
=12kx2
=12(50Nm−1×0.05m×0.05m)
=0.0625J
The total energy of the block at x = 5 cm,
= K.E. + P.E.
= 0.25 J
we also know that at maximum displacement, K.E. is zero and hence the total energy of the system is equal to the P.E. Therefore, the total energy of the system,
=12(50Nm−1×0.1m×0.1m)
=0.25J
which is same as the sum of the two energies at a displacement of 5 cm. This is in conformity with the principle of conservation of energy.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercises
27 Videos
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
3 Videos
Similar Questions
Which of the following examples represent periodic motion?
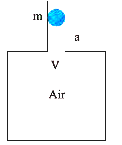
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
View SolutionThe instantaneous speed of the point of contact during rolling is zero.
View SolutionA block of mass one kg is fastened to a spring with a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Write the expression for its x(t) and v(t).
View SolutionA block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0. Calculate the kinetic, potential and total energies of the blocak when it is 5cm away from the mean position.
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm^(-1) . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50Nm−1. The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0. What is the magnitude a_(m) of the maximum acceleration of the block?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the displacement function x(t) for the spring block system?
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50 N m^(-1) . The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm^(-1) . The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0 . Calculate the kinetic, potential and total energies of the block when it is 5cm away from the mean position.
View SolutionA block whose mass is 1kg is fastened to a spring. The spring has a spring constant of 50Nm−1. The block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass is 2kg is fastened to a spring. The spring has a spring constant of 100 Nm^(-1) . The block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View Solution
