A body oscillates with SHM according to the equation (in SI units),
x=5cos[2πt+π/4].
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.Solution in Bengali
The angular frequency ω of the body =2πs−1 and its time period T = 1 s.
At t = 1.5 s
(a) displacement = (5.0 m) cos [(2πs−1×1.5s+π/4]
=(5.0m)cos[(3π+π/4)]
=05.0×0.707m
=−5.0×0.707m
=3.535m
(b) Using Eq. (14.9), the speed of the body
=−(5.0m)(2πs−1)sin[(2πs−1)sin[(2πs−1)×1.5s+π/4]
=−(5.0m)(2πs−1)sin[(3π+π/4)]
=10π×0.707ms−1
=22ms−1
(c) Using Eq.(14.10), the acceleration of the body
=−(2πs−1)2× displacement
=−(2πs−1)2×(−3.535m)
=140ms−2
Topper's Solved these Questions
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercises27videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES5videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)3videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Which of the following examples represent periodic motion?
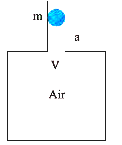
09:01View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 01:08View Solution
01:08View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
09:01View SolutionThe instantaneous speed of the point of contact during rolling is zero.
01:52View SolutionA body oscillates with SHM, accroding to the equation, x=(5.0m)cos[(2pi t+pi//4] At t=1.5s , calculate the (a) diplacement (b) speed and (c) acceleration of the body.
06:54View SolutionA body oscillates with SHM according to the equation (in SHM unit ), x=5"cos"(2pit+(pi)/(4)) . Its instantaneous displacement at t=1 s is
03:25View Solutionकोई पिंड निम्नलिखित समीकरण के अनुसार सरल आवृत गति से दोलन करता है,
x=(5.0m)cos[(2πrad/s)t+π/4].
t = 1.5 s पर, पिंड का (a) विस्थापन, (b) वेग तथा ( c ) त्वरण परिकलित कीजिए |03:25View Solutionकोई पिण्ड निम्नलिखित समीकरण के अनुसार सरल आवर्त गति से दोलन करता है
x= 5cos[(2pi rad/s)t + pi/4]
t= 1.5s पर, पिण्ड का विस्थापन परिकलित कीजिये।03:25View SolutionA body oscillates with simple periodic motion according to the following equation The x = (5.0m) cos [(2pi red//s) t + pi//4] t =1.5 s But, calculate (a) displacement of the body, (b) velocity and (c) acceleration.
03:25View SolutionA body oscillates with SHM according to the equation (in SI units),
x=5cos[2πt+π/4].
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.01:16View SolutionA body oscillates with SHM according to the equation (in SI units),
x=5cos[2πt+π/4].
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.02:04View SolutionA body oscillates with SHM according to the equation (in SI units),
x=5cos[2πt+π/4].
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.01:33View SolutionA body oscillates with SHM according to the equation (in SI units),
x=5cos[2πt+π/4].
At t = 1.5 s, calculate the (a) displacement, (b) speed and (c) acceleration of the body.View SolutionA body oscillator with SHM according to the equation (in SI units) x= 10cos [2pi t +(pi)/(4)] At t= 1.5s calculate the displacement.
05:13View SolutionA body oscillator with SHM according to the equation (in SI units) x= 10cos [2pi t +(pi)/(4)] At t= 1.5s calculate the speed.
View Solution

