A resistance of draws current from a potentiometer. The potentiometer has a total resistance voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
 Solution in Kannada
Solution in Kannada
While the slide is in the middle of the potentiometer only half of its resistance will be between the points A and B. Hence, the total resistance betweeen A and B, say, will be given by the following expression:
The total resistance between A and C will be the sum of resistance between A and B,B and C, i.e.,
The current flowing through the potentiometer will be
The voltage taken from the potentiometer will be product of current I and resistance
Substituting for we have a
Topper's Solved these Questions
- CURRENT ELECTRICITY Book:OSWAAL PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:TOPIC-3 (POTENTIOMETER & APPLICATIONS) (LONG ANSWER TYPE QUESTION)
Explore 1 Video
- COMMUNICATION SYSTEMBook:OSWAAL PUBLICATIONChapter:COMMUNICATION SYSTEMExercise:TOPIC-3 INTERNET, MOBILE AND GPS (SHORT ANSWER TYPE QUESTIONS -I)
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:OSWAAL PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTERExercise:TOPIC-2 DE-BROGLIE RELATION (NUMERICAL PROBLEMS)
Explore 7 Videos
Similar Questions
Write the principle of working of a potentiometer. Describe briefly, with the help of circuit diagram, how a potentiometer is used to determine the internal resistance of a given cell.
View SolutionArrange the following networks in increasing order of the number of computers that may be present in the network:
Internet, LAN, WAN
View SolutionCalculate de-Broglie wavelength associated with a rifle bullet of mass 2 gram moving with a speed of 400ms−1.
View Solution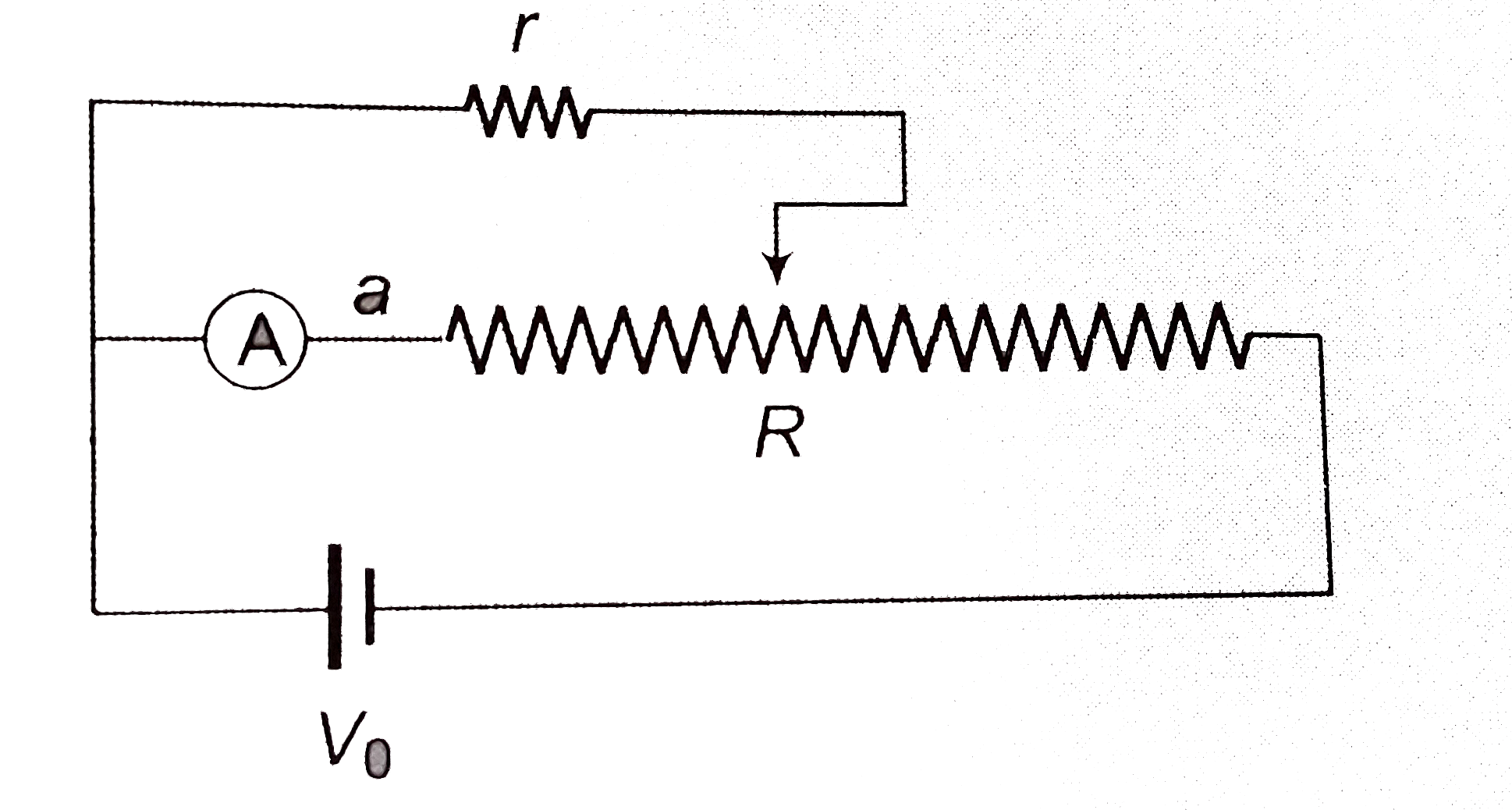
A constant voltage V0 is applied to a potentiometer of resistance R connected to an ammeter. A constant resistor r is connected to the sliding contact of the potentiometer and the fixed end of the potentiometer. How will the reading of ammeter vary as the sliding contact is moved from one end of the potentiometer to the other ? The resistance of ammeter is assumed to be negligible.
View SolutionRΩ का कोई प्रतिरोध एक पोटेंशियोमीटर से विघुत धारा प्राप्त कर रहा है पोटेंशियोमीटर का कुल प्रतिरोध R0Ω है । ( चित्र 3 .29 ) पोटेंशियोमीटर को वोल्टता V की आपूर्ति की गयी है l जब सर्पी संपर्क ( सरकने वाला भाग या स्लाइड ) पोटेंशियोमीटर के तार के मध्य के हो तो R के सिरों पर वोल्टता के लिए व्यंजक प्राप्त कीजिए l

View SolutionA resistance of RΩ draws current from a potentiometer. The potentiometer has a total resistance R0Ω. A voltage V is supplied to the potentiometer. Dervie can expression for the voltage across R when the sliding contact is in the middle of the potentiometer.

View SolutionRΩ का एक प्रतिरोध एक विभवमापी से विद्युत धारा प्राप्त कर रहा है । विभवमापी का कुल प्रतिरोध R0Ω है । विभवमापी को वोलटता V की आपूर्ति की गई है । जब सप्री संपर्क ( सरकने वाले भाग या स्लाइड ) विभवमापी के तार के मध्य में हो , तो R के सिरों पर वोलटता के लिए व्यंजक प्राप्त कीजिए ।
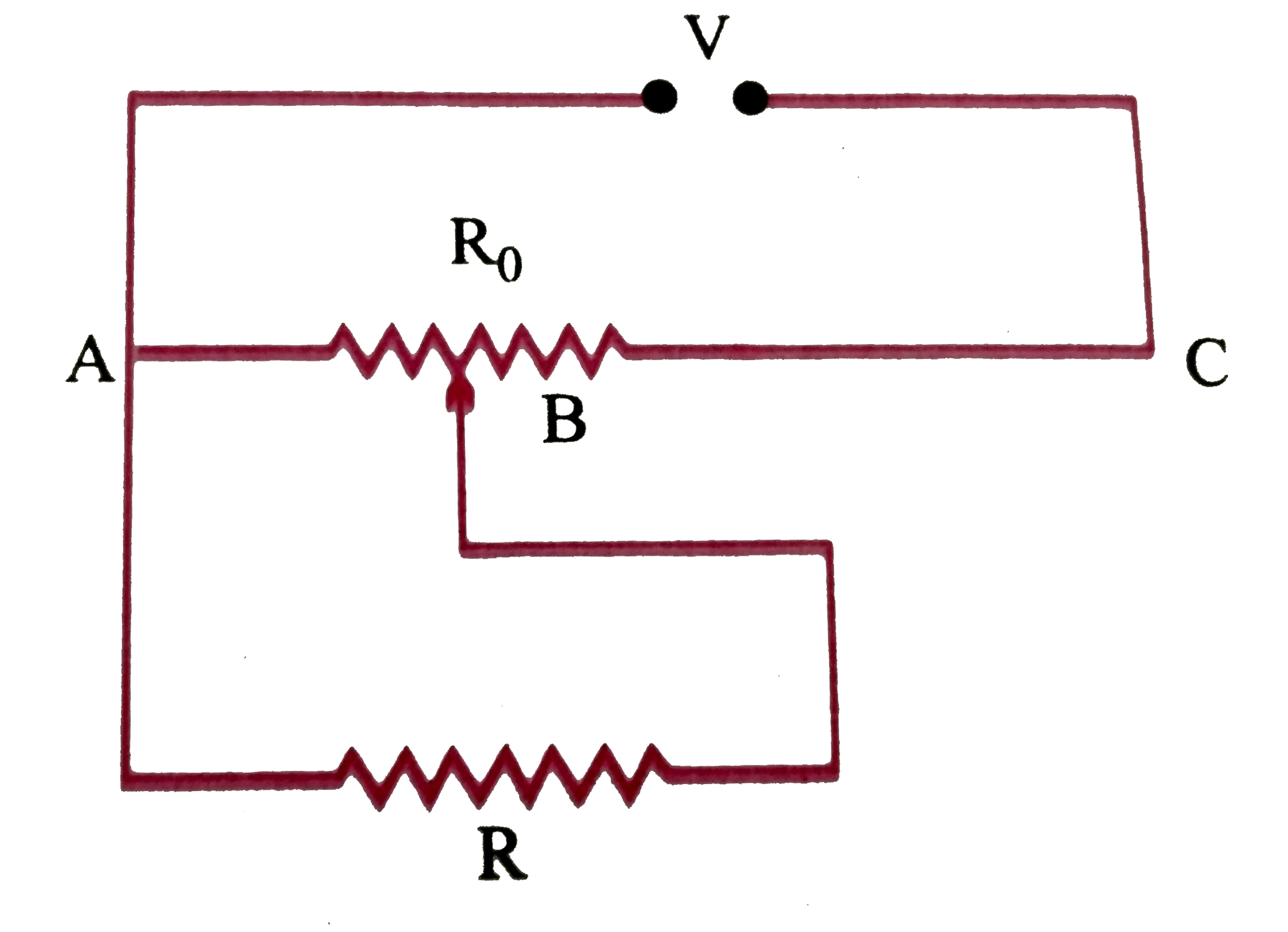
View SolutionRΩ का कोई प्रतिरोध एक विभवमापी से विद्युत धारा प्राप्त कर रहा है। विभवमापी का कुल प्रतिरोध R0Ω है। विभवमापी को वोल्टता V की आपूर्ति की गई है। जब सर्पी सम्पर्क (सरकने वाला भाग या स्लाइड) विभवमापी के तार के मध्य में हो R के सिरों पर वोल्टता के लिए व्यंजक प्राप्त कीजिए।
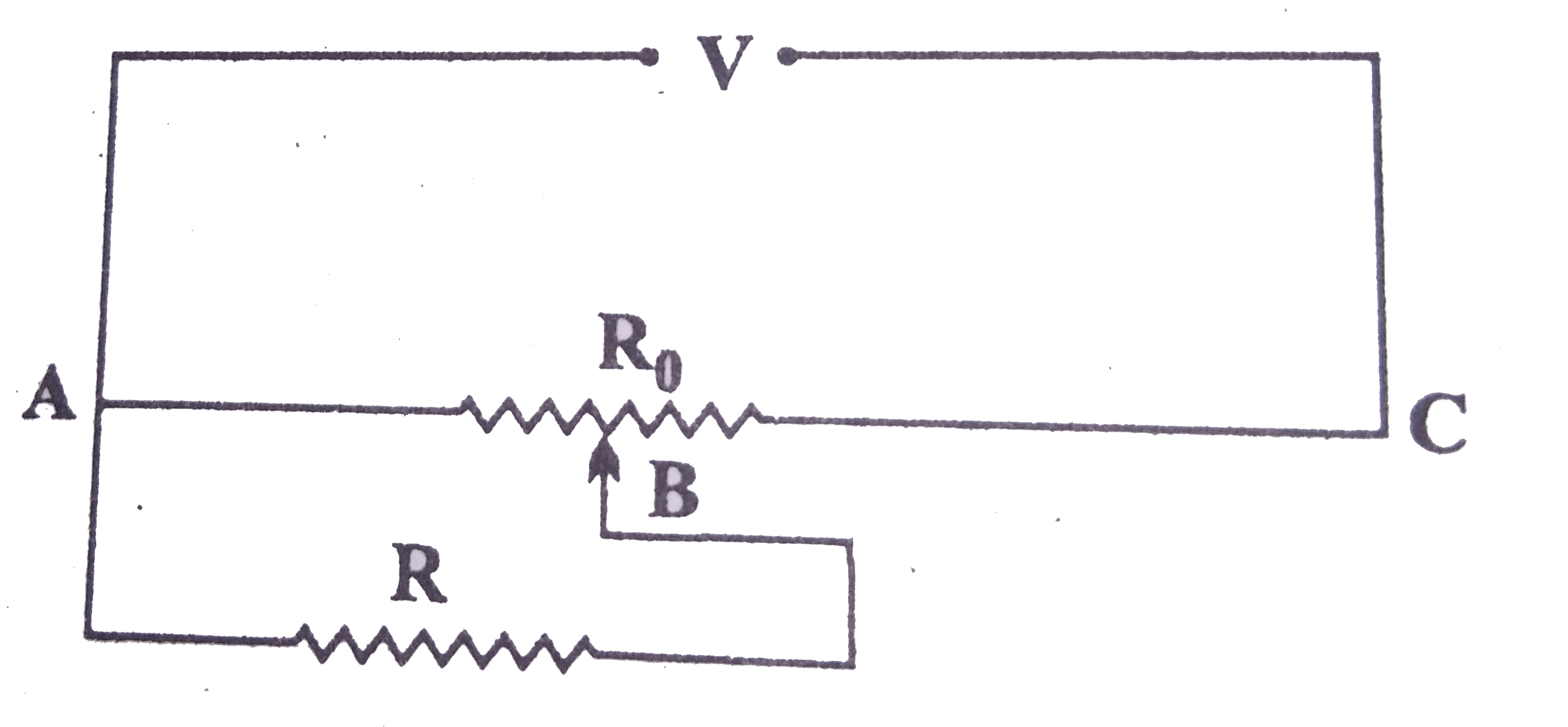
View SolutionA resistance of R draw current from a potentiometer. The potentiometer wire, AB, has total resistance of R0. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire.
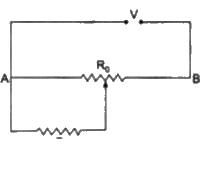
View SolutionIn a potentiometer experiment if the voltage across resistance R and R + r are balanced at the length l1andl2 respectively the value of resistance r will be
View SolutionA resistance of R Omega draws current from a potentiometer as shown in Fig. The potentiometer has a total resistance R_0 Omega . A voltage Vis supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
View SolutionA rsisitance of RΩ draws current from a potentiometer. Te potentiometer has a total resistance R0Ω A voltage V is supplited to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potenttometer.
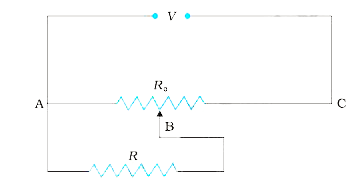
View SolutionA resistance of R draws current from a potentiometer. The potentiometer wire, AB , has a total resistance of R0, A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentialmeter wire.

View SolutionA voltage V is supplied to a potentiometer wire of resistance R_0 . A resistance R is connected as shown. Find voltage across R when the sliding contact is at the middle of potentiometer wire
View SolutionA resistance of Rω draws current from a potentiometer. The potentio - meter has a total resistance R0Ω (Fig). A voltage V is supplied to the potentiometer.
Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
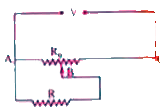
View Solution

