The uniform rod (length 0.60 m, mass 1.0 kg) in Fig. 10-85 rotates in the plane of the figure about an axis through one end, with a rotational inertia of 0.12kg⋅m2. As the rod swings through its lowest position, it collides with a 0.20 kg putty wad that sticks to the end of the rod. If the rod's angular speed just before collision is 2.4 rad/s, what is the angular speed of the rod-putty system immediately after collision?

1.5 rad/s
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS - IExercise:PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
Explore 43 Videos
- RIGID BODY DYNAMICS - IBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS - IExercise:PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
Explore 7 Videos
- RIGID BODY DYNAMICS - IBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS - IExercise:CHECKPOINT
Explore 18 Videos
- RELATIVITYBook:RESNICK AND HALLIDAYChapter:RELATIVITYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
- RIGID BODY DYNAMICS-IIBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS-IIExercise:PRACTICE QUESTIONS (Integer Type)
Explore 2 Videos
Similar Questions
A uniform rod of length 1m and mass 0.5kg rotates at angular speed of 6rad/sec about one of its ends. What is the KE (in joule) of the rod ?
View SolutionIn Fig. 10-84, a 1.0 g bullet is fired into a 0.60 kg block attached to the end of a 0.75 m nonuniform rod of mass 0.50 kg. The block-rod-bullet system then rotates in the plane of the figure, about a fixed axis at A. The rotational inertia of the rod alone about that axis at A is 0.060kg⋅m2. Treat the block as a particle. (a) What then is the rotational inertia of the block-rod-bullet system about point A? (b) If the angular speed of the system about A just after impact is 4.5 rad/s, what is the bullet's speed just before impact?

View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
A0.16 kg - m2B0.12 kg - m2C0.32 kg - m2D0.08 kg - m2A uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
Aml23Bml23sinθCml23sin2θDml23cos2θ
A rod of mass 2kg and length 1m is pivoted at one end A and kept on a smooth surface. A particle of mass 500gmstrikestheotherendB of the rod and sticks to the rod. If particle was moving with the speed of 20m/s, what is the angular speed of the rod after collision ?
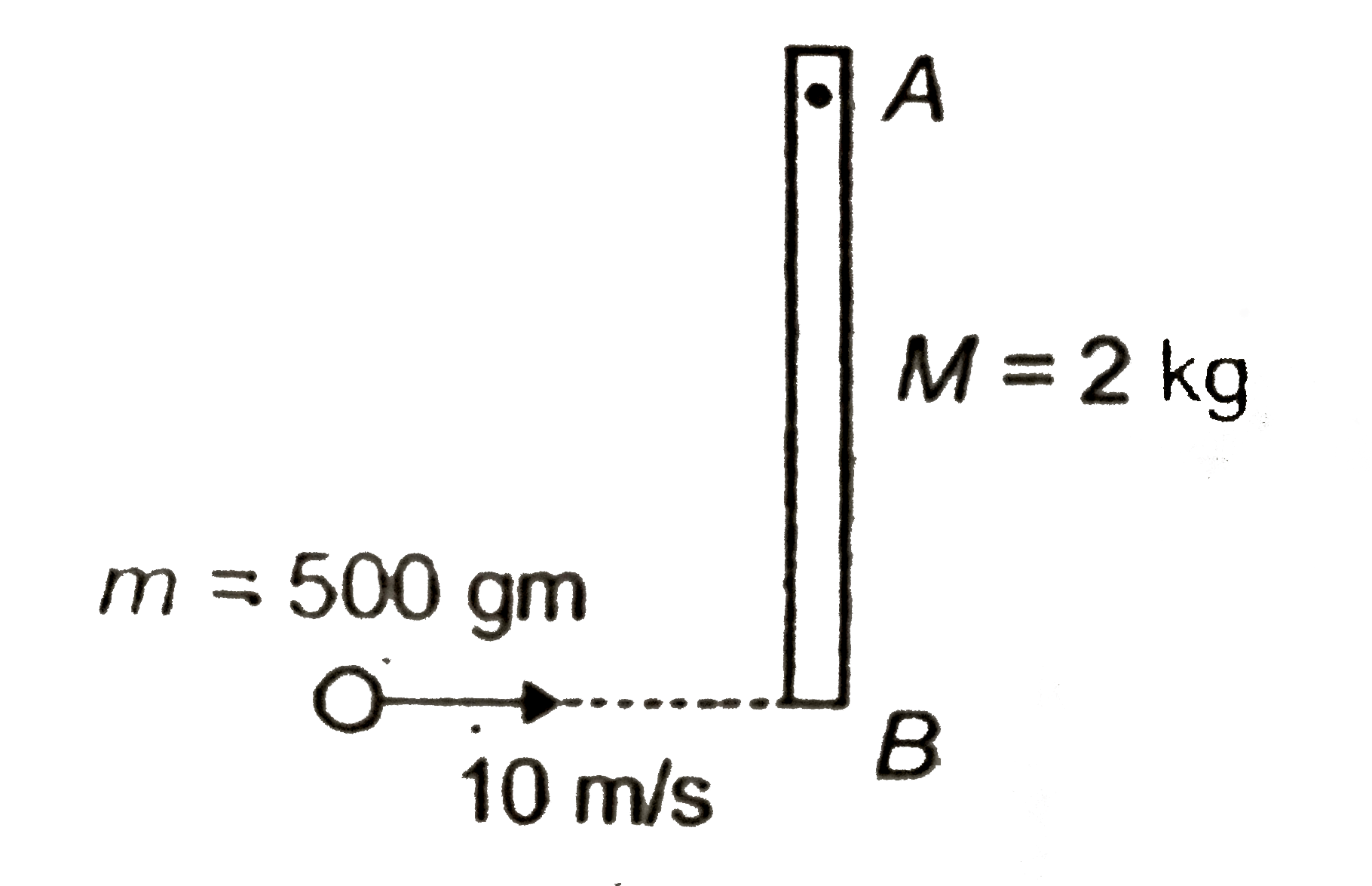
View SolutionA rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionTwo 2.00 kg balls are attached to the ends of a thin rod of length 50.0 cm and negligible mass. The rod is free to rotate in a vertical plane without friction about a horizontal axis through its center. With the rod initially horizontal (Fig. 10-87), a 50.0 g wad of wet putty drops onto one of the balls, hitting it with a speed of 3.00 m/s and then sticking to it. (a) What is the angular speed of the system just after the putty wad hits? (b) What is the ratio of the kinetic energy of the system after the collision to that of the putty wad just before? ( c) Through what angle will the system rotate before it momentarily stops?

View SolutionA metal rod of length 15×10−2m rotates about an axis passing through one end with a uniform angular velocity of 60 rad s−1. A uniform magnetic field of 0.1 Tesla exisits in the direction of the axis of rotationn. Calculate the EMF induced between the ends of the rod.
View SolutionA uniform rod of mass m and length / makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
View Solution

