A 3.0 kg particle-like object moves in a plane with velocity components vx=30m/sandvy=60m/s as is passes through the point with (x, y) coordinates of (3.0, -4.0) m. Just then, in unit vector notation, what is its angular momentum relative to (a) the origin and (b) the point located at (-2.0, -2.0) m?
To solve the problem, we need to calculate the angular momentum of a particle-like object moving in a plane relative to two different points. The object has a mass of 3.0 kg and velocity components vx=30m/s and vy=60m/s. The coordinates of the object at the moment of interest are (3.0,−4.0)m.
Part (a): Angular Momentum Relative to the Origin
1. Determine the position vector r relative to the origin:
r=3^i−4^j
2. Determine the velocity vector v:
v=30^i+60^j
3. Calculate the linear momentum p:
p=mv=3kg⋅(30^i+60^j)=90^i+180^jkg m/s
4. Calculate the angular momentum L using the cross product L=r×p:
L=r×p=(3^i−4^j)×(90^i+180^j)
Using the determinant method for cross products:
L=∣∣
∣
∣∣^i^j^k3−40901800∣∣
∣
∣∣
This results in:
L=(0−0)^i−(0−0)^j+(3⋅180−(−4)⋅90)^k
=(540+360)^k=900^kkg m2/s
Part (b): Angular Momentum Relative to the Point (-2.0, -2.0)
1. Determine the position vector r1 relative to the point (-2, -2):
r1=(3−(−2))^i+(−4−(−2))^j=(3+2)^i+(−4+2)^j=5^i−2^j
2. Use the same velocity vector v as before:
v=30^i+60^j
3. Calculate the angular momentum L1 using the cross product L1=r1×p:
L1=r1×p=(5^i−2^j)×(90^i+180^j)
Using the determinant method for cross products:
L1=∣∣
∣
∣∣^i^j^k5−20901800∣∣
∣
∣∣
This results in:
L1=(0−0)^i−(0−0)^j+(5⋅180−(−2)⋅90)^k
=(900+180)^k=1080^kkg m2/s
Final Answers
- (a) Angular momentum relative to the origin: L=900^kkg m2/s
- (b) Angular momentum relative to the point (-2, -2): L1=1080^kkg m2/s
r=3^i−4^j
v=30^i+60^j
p=mv=3kg⋅(30^i+60^j)=90^i+180^jkg m/s
L=r×p=(3^i−4^j)×(90^i+180^j)
L=∣∣
∣
∣∣^i^j^k3−40901800∣∣
∣
∣∣
L=(0−0)^i−(0−0)^j+(3⋅180−(−4)⋅90)^k
=(540+360)^k=900^kkg m2/s
r1=(3−(−2))^i+(−4−(−2))^j=(3+2)^i+(−4+2)^j=5^i−2^j
v=30^i+60^j
L1=r1×p=(5^i−2^j)×(90^i+180^j)
L1=∣∣
∣
∣∣^i^j^k5−20901800∣∣
∣
∣∣
L1=(0−0)^i−(0−0)^j+(5⋅180−(−2)⋅90)^k
=(900+180)^k=1080^kkg m2/s
- (a) Angular momentum relative to the origin: L=900^kkg m2/s
- (b) Angular momentum relative to the point (-2, -2): L1=1080^kkg m2/s
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
43 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A motorbike starts from the origin and moves over an xy plane with acceleration components ax=6.0m/s2anday=−3.0m/s2. The initial velocity of the motorbike has components v0x=12.0m/sandv0y=18.0m/s. Find the velocity of the motorbike, in unt-vector notation, when it reaches its greatest y coordinate.
View SolutionA particle starts from the origin at t=0 with a velocity of 8.0ˆjm/s and moves in the x-y plane with a constant acceleration of (4.0ˆi+2.0ˆj)m/s2. At the instant the particle's x-coordinate is 29 m, what are
(a) its y-coordinate and
(b) its speed ?
View Solution
Knowledge Check
A 2.0-kg projectile is fired with initial velocity components vox=30m/s and voy=40m/s from a point on the earth's surface. Neglect any effects due to air resistance.
What is the kinetic energy of the projectile when it reaches the highest point in its trajectory ?AzerojoulesB1600JC900JD2500JA 2.0-kg projectile is fired with initial velocity components vox=30m/s and voy=40m/s from a point on the earth's surface. Neglect any effects due to air resistance.
How much work was done in firing the projectile ?A900JB2500JC1600JD4900JThe point (x,y) lies on the line with slope m and passes through the fixed point (x0,y0) if and only if its coordinates satisfy the equation y−y0 is equal to
Am(x−x0)Bm(y−x0)Cm(y−x)Dm(x−y0)
Force →F=(2.0N)ˆi−(3.0N)ˆk acts on a pebble with position vector →r=(0.50m)ˆj−(2.0m)ˆk relative to the origin. In unit-vector notation, what is the resulting torque on the pebble about the origin ?
View SolutionTwo particles A and B are moving in the x−y plane such that their velocity components are vx=1m/s,vy=1√3m/s (for A) and vx=2m/s,vy=2m/s (for B). If both the particles start moving from the same point, what is the angle between their paths ?
View SolutionDistance of point P on the curve y=x3/2 which is nearest to the point M (4, 0) from origin is
View SolutionA particle starts from the point (0m,8m) and moves with uniform velocity of 3ˆim/s. After 5 seconds, the angular velocity of the particle about the origin will be :
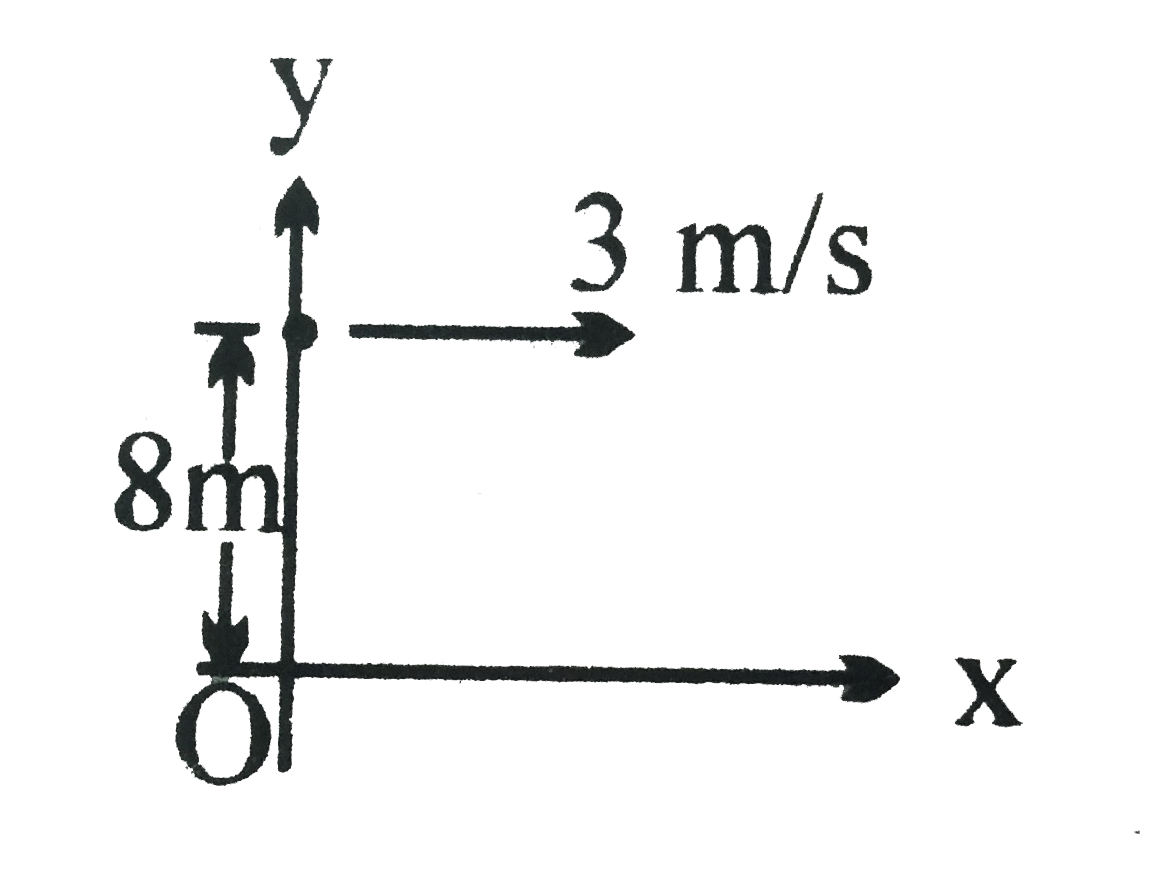 .
.
View SolutionA body of mass 3 kg is moving along the line 5y= 12x +39 with a velocity 5 m/s. At t=0, it is at the point (-2, 3). Find the angular momentum of the particle at t =5 s.
View Solution
