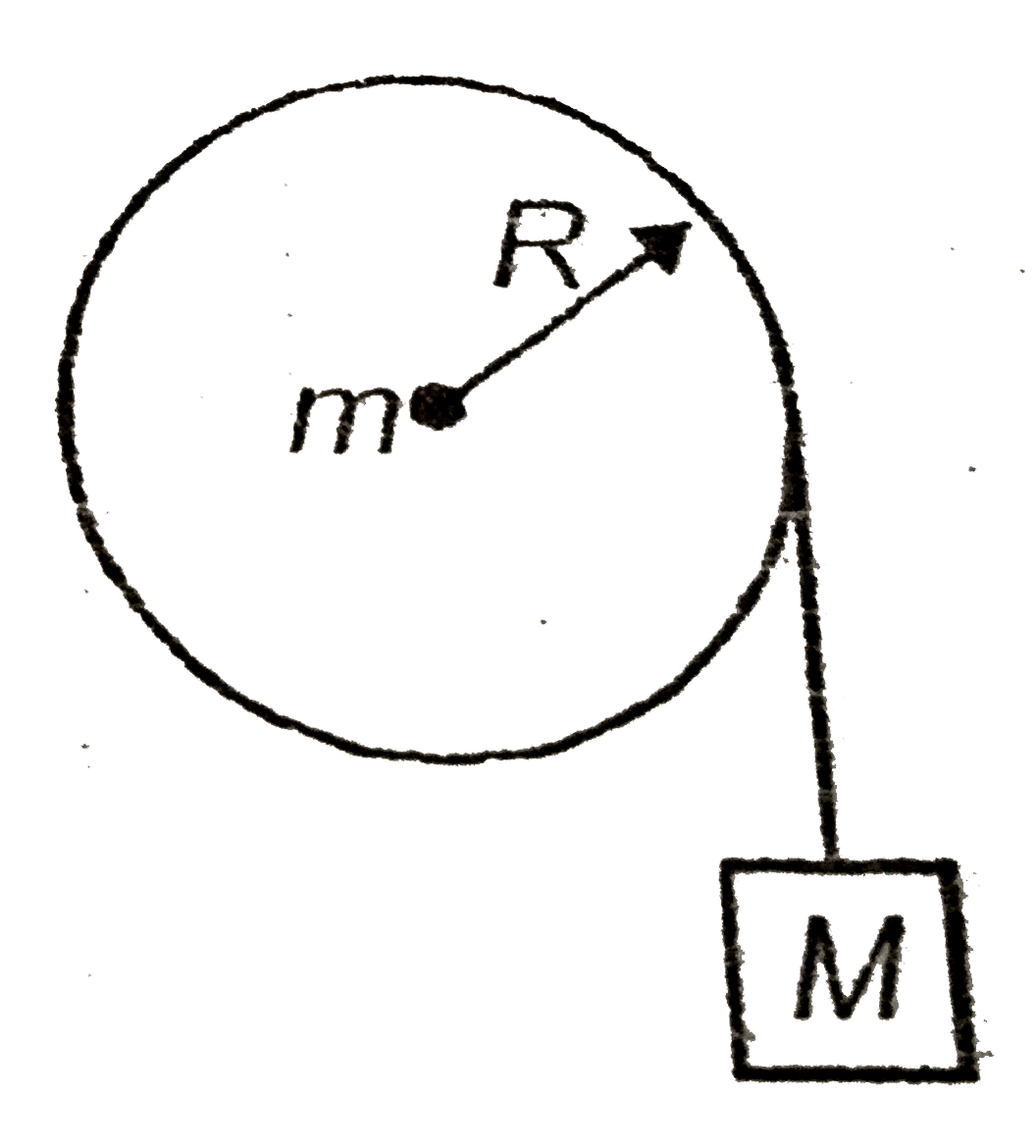
Figure shows a uniform disk, with mass M = 2.5 kg and radius R = 20 cm, mounted on a fixed horizontal axle. A block with mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disk. Find the acceleration of the falling block, the angular acceleration of the disk, and the tension in the cord. The cord does not slip, and there is no friction at the axle.
To solve the problem, we will follow these steps:
Step 1: Analyze the Forces on the Block
The block of mass m is subjected to two forces: the gravitational force mg acting downward and the tension T in the cord acting upward. According to Newton's second law, the net force acting on the block can be expressed as:
mg−T=ma
where a is the acceleration of the falling block.
Step 2: Analyze the Torque on the Disk
The tension T in the cord creates a torque τ on the disk. The torque is given by:
τ=T⋅R
where R is the radius of the disk. The relationship between torque and angular acceleration α is given by:
τ=I⋅α
For a uniform disk, the moment of inertia I is:
I=12MR2
Thus, we can write:
T⋅R=12MR2⋅α
Step 3: Relate Linear and Angular Acceleration
Since the cord does not slip, the linear acceleration a of the block is related to the angular acceleration α of the disk by:
a=αR
From this, we can express α as:
α=aR
Step 4: Substitute α into the Torque Equation
Substituting α into the torque equation gives:
T⋅R=12MR2⋅aR
Simplifying this, we find:
T=12Ma
Step 5: Substitute T into the Block's Equation
Now we substitute T back into the equation for the block:
mg−12Ma=ma
Rearranging this gives:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Thus, we can solve for a:
a=mgm+12M
Step 6: Plug in the Values
Now we can substitute the given values into the equation. We have:
- m=1.2kg
- M=2.5kg
- g=10m/s2
Substituting these values:
a=(1.2)(10)1.2+12(2.5)=121.2+1.25=122.45≈4.898m/s2
Step 7: Calculate Angular Acceleration α
Using the relationship a=αR:
α=aR
Converting R=20cm=0.2m:
α=4.8980.2=24.49rad/s2
Step 8: Calculate Tension T
Using the expression for T:
T=12Ma
Substituting the values:
T=12(2.5)(4.898)≈6.123N
Final Results
- Acceleration of the falling block a≈4.898m/s2
- Angular acceleration of the disk α≈24.49rad/s2
- Tension in the cord T≈6.123N
The block of mass m is subjected to two forces: the gravitational force mg acting downward and the tension T in the cord acting upward. According to Newton's second law, the net force acting on the block can be expressed as:
mg−T=ma
where a is the acceleration of the falling block.
The tension T in the cord creates a torque τ on the disk. The torque is given by:
τ=T⋅R
where R is the radius of the disk. The relationship between torque and angular acceleration α is given by:
τ=I⋅α
For a uniform disk, the moment of inertia I is:
I=12MR2
Thus, we can write:
T⋅R=12MR2⋅α
Since the cord does not slip, the linear acceleration a of the block is related to the angular acceleration α of the disk by:
a=αR
From this, we can express α as:
α=aR
Substituting α into the torque equation gives:
T⋅R=12MR2⋅aR
Simplifying this, we find:
T=12Ma
Now we substitute T back into the equation for the block:
mg−12Ma=ma
Rearranging this gives:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Thus, we can solve for a:
a=mgm+12M
Now we can substitute the given values into the equation. We have:
- m=1.2kg
- M=2.5kg
- g=10m/s2
a=(1.2)(10)1.2+12(2.5)=121.2+1.25=122.45≈4.898m/s2
Using the relationship a=αR:
α=aR
Converting R=20cm=0.2m:
α=4.8980.2=24.49rad/s2
Using the expression for T:
T=12Ma
Substituting the values:
T=12(2.5)(4.898)≈6.123N
- Acceleration of the falling block a≈4.898m/s2
- Angular acceleration of the disk α≈24.49rad/s2
- Tension in the cord T≈6.123N
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
Figure shows a uniform disk, with mass M=2.4kg and radius R=20 m, mounted on a fixed horizontal axle. A block of mass m=1.2 kg hangs from a massless cord that is wrapped around the rim of the disk. The tension (in newton) in cord. Is
'(##CEN_KSR_PHY_JEE_C09_E01_019_Q09##)'
View SolutionTwo blocks of mass 2 kg and 5 kg are connected by an ideal string passing over a pulley. The block of mass 2 kg is free to slide on a surface inclined at an angle of 30∘ with the horizontal whereas 5 kg block hangs freely. Find the acceleration of the system and the tension in the string.
View Solution
Knowledge Check
The figure shows a uniform disc, with mass M = 2.4 kg and radius R= 20 cm, mounted on a fixed horizontal axle. A block of mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disc. The tension in the cord is
 A12 NB20 NC24 NDnone of these
A12 NB20 NC24 NDnone of theseA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
A2MM+2mgB2mM+2mgCM+2m2MgD2M+m2MgA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
ATMRBMRTC2TMRDMR2T
A disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionA uniform disc of radius R and mass M is mounted on an axis supported in fixed friction less bearing. A light cord is wrapped around the rim of the wheel and suppose we hang a body of mass m from the cord.
(a) Find the angular acceleration of the disc and tangential acceleration ofpoint on the rim.
(b) At a moment t= 0, the system is set in motion, find the time dependence of the angular velocity of the system and the kinetic energy ofthe whole system.
View SolutionFigure 5-20 shows a block S (the sliding block) with mass M = 3.3 kg. The block is free to move along a horizontal frictionless surface and connected, by a cord that wraps over a frictionless pulley, to a second block H (the hanging block), with mass m = 2.1 kg. The cord and pulley have negligible masses compared to the blocks (they are "massless"). The hanging block H falls as the sliding block S accelerates to the right. Find (a) the acceleration of block S, (b) the acceleration of block H, and ( c ) the tension in the cord.
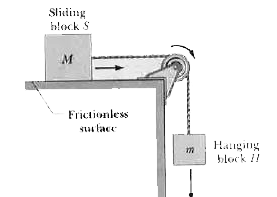
Figure 5.20 A block S of mass M is connected to a block H of mass m by a cord that wraps over a pulley.
View SolutionA uniform disc of mass 2 kg and radius 1m is mounted on an axle supported on fixed frictionless bearings. A light chord is wrapped around the rim of the disc and mass of 1kg is tied to the free end. If it is released from rest-
View SolutionA string is wound round the rim of a mounted flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel is
View Solution
