Find the moment of inertia of a uniform rign of mass M and radius R about a diameter.

Video Solution

Text Solution

Verified by Experts

The total mass M is given by the integral of the surface density $σ$ over the area of the shell $M = \int σ d A$ . Since the shell is homogeneous, the surface density $σ$ is constant.
Therefore,
$M = \int σ d A = σ A = 4 π R^{2} σ$ .
This implies that
$\sum = \frac{M}{4 π r^{2}}$ .
Calculations: In the fig. the hoop shown has a radius $r = R sin θ$ and therefore a circumference of $2 π R sin θ$ . The width of the hoop is $R d θ$ , so the area $d A = (2 π R sin θ) (R d θ)$ , and the mass $d M = σ d A = (M / 4 π R^{2}) (2 R^{2} sin θ d θ) = (M / 2) sin θ d θ$ .

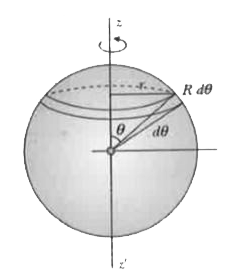
We use dI to denote the moment of inertia of the hoop about the axis zz.. The perpendicular distance from the axis to each part of the hoop is $R sin θ$ . Therefore, $d I = d m {(R sin θ)}^{2} and d M = (M R^{2} l^{2}) {sin}^{3} θ d θ$ . The moment of inertia of the entire shell is the sum of moment of inertia of the various hoops.
$d l = \frac{M}{2} sin θ d θ R^{2} {sin}^{2} θ$ .
Integrating over whole sphere, we get
$I = \frac{M R^{2}}{2} \int_{0}^{π} {sin}^{3} θ d θ$ .
We can write as
${sin}^{3} θ = \frac{- sin 3 θ + 3 sin θ}{4}$ .
Substituting in the above equation, we get
$I = \frac{M R^{2}}{8} [\int_{0}^{π} sin 3 θ d θ + 3 \int_{0}^{π} sin θ d θ]$
= $\frac{M R^{2}}{8} [- \frac{2}{3} + 6]$
= $\frac{2}{3} M R^{2}$ .
We have derived the result by adding moment of inertia of hoops.

Updated on:21/07/2023

Moment of inertia of a circular wire of mass M and radius R about its diameter is
A $M \frac{R^{2}}{2}$
B $M R^{2}$
C $2 M R^{2}$
D $M \frac{R^{2}}{4}$
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
A $\frac{M R^{2}}{2}$
B $\frac{M R^{2}}{4}$
C $\frac{M R^{2}}{3}$
D $\frac{M R^{2}}{12}$
The moment of inertia of a thin circular disc of mass M and radius R about any diameter is
A $\frac{M R^{2}}{4}$
B $\frac{M R^{2}}{2}$
C $M R^{2}$
D $2 M R^{2}$