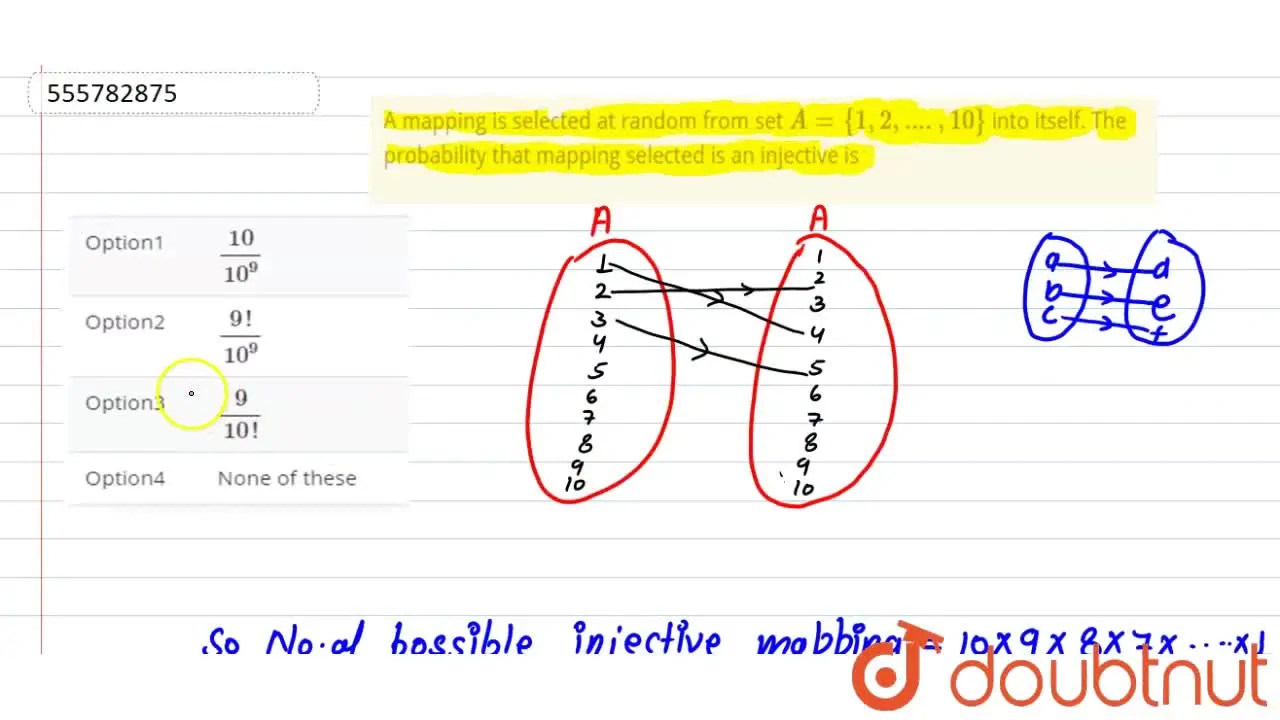
A mapping is selected at random from set A={1,2,....,10} into itself. The probability that mapping selected is an injective is
10109
9!109
910!
None of these
The correct Answer is:B
Step by step video, text & image solution for A mapping is selected at random from set A={1, 2, ...., 10} into itself. The probability that mapping selected is an injective is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type ( 2 Marks) )14videos
STATISTICS AND PROBABILITY
- BOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type ( 2 Marks) )15videos
STATISTICS AND PROBABILITY
- BOOK - MTG-WBJEECHAPTER - SOLUTION OF TRIANGLESEXERCISE - WB JEE (Previous Years Questions) CATEGORY 2: Single Option Correct Type1videos
SOLUTION OF TRIANGLES
- BOOK - MTG-WBJEECHAPTER - STRAIGHT LINESEXERCISE - WB JEE Previous Years Questions28videos
STRAIGHT LINES
Similar Questions
Let A and B be two finite sets having m and n elements respectively such that m≤n. A mapping is selected at random from the set of all mappings from A to B. The probability that the mapping selected is an injection, is
View SolutionOne mapping is selected at random from all mappings of the set S={1,2,3,n} into itself. If the probability that the mapping is one-one is 3/32, then the value of n is 2 b. 3 c. 4 d. none of these
View SolutionOne mapping is selected at random from all mappings of the set S={1,2,3,n} into itself. If the probability that the mapping is one-one is 3/32, then the value of n is 2 b. 3 c. 4 d. none of these
View SolutionA mapping is selected at random from all mappings f:A rarr A where set A={1,2,3,....n}If the probability that mapping is injective is 332 then the value of n is:
View SolutionA number is selected at random from the set {1, 2, 3, ........ , 50}. The probability that it is a prime, is
View SolutionA mapping is select at random from the set of all the mappings of the set A={1,2,n} into itself. Find the probability that the mapping selected is an injection.
View SolutionOne mapping (function) is selected at random from all the mappings of the set A ={1,2,3,…..,n} into itself. The probability that the mapping selected is one -one ,is
View SolutionA number is selected at random from the set {1, 2, 3, …, 50}. The probability that it is a prime, is
View Solution36. One mapping /function is selected at random from all the mappings of the set A = {1,2,3,4,5). Into itself. Find the probability that the mapping selected is one to one.
View SolutionIn above question if m>n then the probability that the mapping selected is an injective mapping is :
View Solution