The equation out of four maxweel's equations which show (s) electric field lines do not form closed loops is/are

A

$\oint_{s} \vec{E} . \bar{d s} = q / ε_{0}$

B

$\oint_{s} \bar{B} . \bar{d} s = 0$

C

$\oint \bar{E} . d \bar{t} = \frac{d ϕ_{B}}{d t}$

D

None of these

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To determine which of Maxwell's equations indicates that electric field lines do not form closed loops, we can analyze each of the four equations.
1. Identify Maxwell's Equations:
The four Maxwell's equations are:
- Gauss's Law: $\oint E \cdot d s = \frac{Q_{enc}}{ϵ_{0}}$
- Gauss's Law for Magnetism: $\oint B \cdot d s = 0$
- Faraday's Law of Induction: $\oint E \cdot d s = - \frac{d Φ_{B}}{d t}$
- Ampère-Maxwell Law: $\oint B \cdot d s = μ_{0} I_{enc} + μ_{0} ϵ_{0} \frac{d Φ_{E}}{d t}$
2. Analyze Gauss's Law:
Gauss's Law states that the electric flux through a closed surface is proportional to the charge enclosed. This implies that electric field lines originate from positive charges and terminate at negative charges, indicating that they do not form closed loops.
3. Analyze Gauss's Law for Magnetism:
This law states that the magnetic flux through a closed surface is zero, indicating that magnetic field lines do form closed loops.
4. Analyze Faraday's Law of Induction:
This law indicates that a changing magnetic field induces an electric field. The line integral of the electric field around a closed loop is related to the rate of change of magnetic flux, which suggests that electric field lines can be induced but do not form closed loops on their own.
5. Analyze Ampère-Maxwell Law:
This law relates the magnetic field to the current and the rate of change of electric field. It also implies that magnetic field lines can form closed loops.
6. Conclusion:
From the analysis, we can conclude that Gauss's Law is the equation that shows that electric field lines do not form closed loops. Therefore, the correct answer is:
Answer: Gauss's Law ( $\oint E \cdot d s = \frac{Q_{enc}}{ϵ_{0}}$ )

Updated on:18/9/2024

|

Class 12 PHYSICS ELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Drawings I and II show to samples of electric field lines

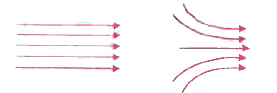AThe electric fields in both I and I I are produced by negative charge located somewhere on the left and positive charges located somewhere on the right
BIn both I and II the electric field is the same every where
CIn both cases the field becomes stronger on moving form left to righ
DThe electric field in I is the same everywhere, but in II the electric field becomes stronger on moving from left to right.
Out of the four Maxwell's equations above, which one shows non-existence of monopoles?
A( $i$ ) and ( $i v$ )
B( $i i$ ) only
C( $i i i$ ) only
Dnone of these
Drawings $I$ and $I I$ show two samples of electric field lines

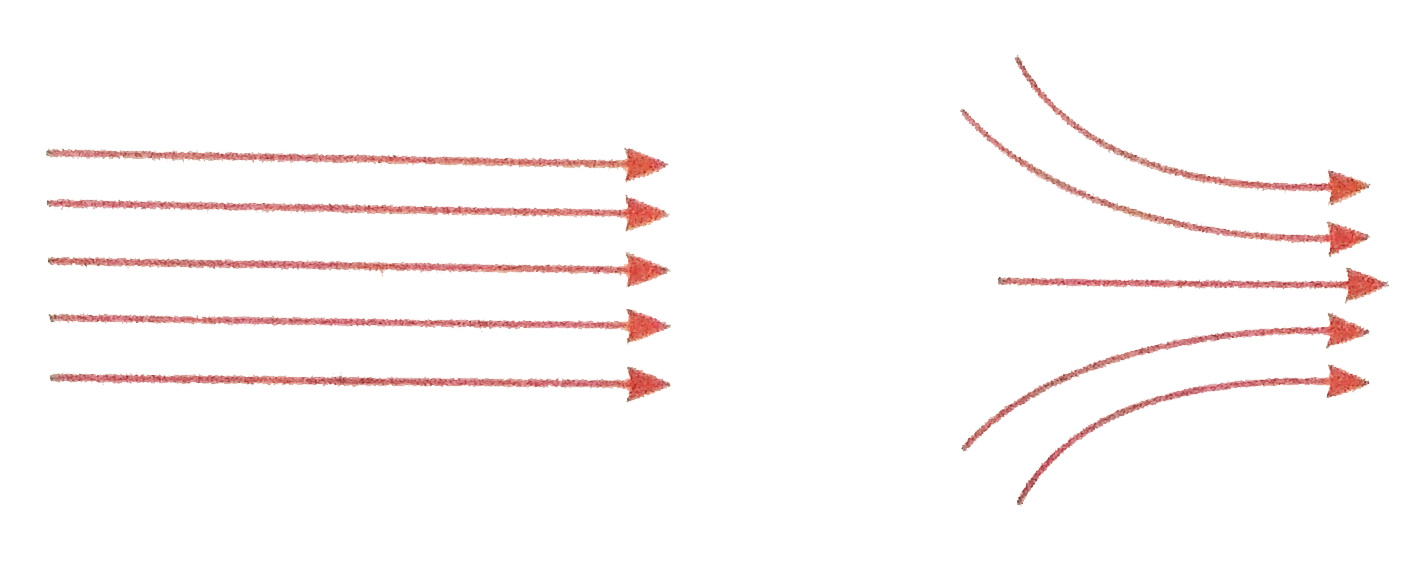AThe electric fields in both I and II are produced .by negative charge located somewhere on the left and positive charges located somewhere on the right
BIn both I and II the electric field is same every where
CIn both cases the field becomes stronger on moving form left to right
DThe electric field in I is the same everywhere ,but in II the electric field becomes stronger on moving from left and right

MTG-WBJEE-ELECTROMAGNETIC WAVES -WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)

Home
Ask Doubt
Profile