The density of water is 1g/mL. Assuming that there are no intermolecular spaces between water molecules in liquid water, the volume of a water molecule is Solution in Telugu
1.5×10−23 ml
6×10−23ml
3×10−23ml
3×10−22ml
The correct Answer is:C
Step by step video, text & image solution for The density of water is 1g/mL. Assuming that there are no intermolecular spaces between water molecules in liquid water, the volume of a water molecule is by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STOICHIOMETRYBook:AAKASH SERIESChapter:STOICHIOMETRYExercise:PRACTICE SHEET (EXERCISE-I LEVEL-II MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
Explore 5 Videos
- STOICHIOMETRYBook:AAKASH SERIESChapter:STOICHIOMETRYExercise:PRACTICE SHEET (EXERCISE-I LEVEL-II LINKED COMPREHENSION TYPE QUESTIONS)
Explore 7 Videos
- STOICHIOMETRYBook:AAKASH SERIESChapter:STOICHIOMETRYExercise:PRACTICE SHEET (EXERCISE-I LEVEL-I STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 10 Videos
- STATES OF MATTER Book:AAKASH SERIESChapter:STATES OF MATTER Exercise:ADDITIONAL PRACTICE EXERCISE -PRACTICE SHEET (ADVANCED) (LINKED COMPREHENSION TYPE QUESTIONS) (PASSAGE- IV)
Explore 2 Videos
- SURFACE CHEMISTRYBook:AAKASH SERIESChapter:SURFACE CHEMISTRYExercise:Objective Excersice - 4 (ASSERTION (A)& REASON (R ) TYPE QUESTION)
Explore 34 Videos
Similar Questions
6.023×1022 atoms of Hydrogen can make
View SolutionAvogadro's lasw states that under conditions of constant temp. and pressure equal volume of gases contain equal no. of particles. Experimental investigation shows that at one atmosphere pressure and a temperature of 273 k, one mole of any gas occupies a volume of which is very close to 22.4 lit. Therefore, the number of moles in any gas sample canbe found by comparing its volume at STP with 22.4 lit.
If avagadro's number is 6×1023 molecules then the mass of one atom of oxygen would be
View SolutionOne mole of sodium represents
View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
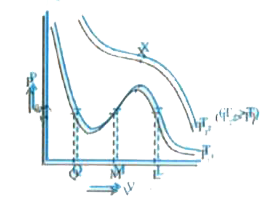
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as
View Solution(A) De-emulsification is a reverse process of emulsion formation
(R ) During de-emulsification , the emulsion breaks to give oil and water.
View SolutionThe density of water is 1g/mL. Water is the volume occupied by 1 molecule of water ?
View SolutionAssuming that the density of water to be 1g/cm3, calculate the volume occupied by one molecule of water.
View SolutionThe density of water is 1gm//ml . The volume of water drop is 1.8 ml. The no. of molecules present in one water drop are
View SolutionVolume occupied one molecule of water (density=1gcm−3) is :-
View Solutionकमरे के ताप पर जल का घनत्व 1.0g/mL है। एक बूँद जल में जल के अणुओ की संख्या ज्ञात करे, जबकि इतने जल का आयतन 0.05mL है।
View Solution(i) Assuming the density of water to be 1g//cm^(3) , calculate the volume occupied by one molecule of water. (ii) Assuming the water molecule to be spherical, calculate the diameter of the water molecule. (iii) Assuming the oxygen atom occupied half of the volume occupied by the water molecule, calculate approximately the diameter of the oxygen atom.
View SolutionHow many water molecules are there in a drop of volume 0.05mL? (Density of water is 1g/mL)
View SolutionVolume occupied by one molecule of water (density = 1g//cm^(3) ) is:
View SolutionThe radius of water molecule having density 1g mL^(-1) is:
View SolutionFind the number of molecules present in 1 liter of water. Also calculate the volume enclosed by a water molecule. (Water density = 1g cm^(-3) )
View Solution

