A periodic transverse wave is established on a string such that there are exactly two cycles traveling along a 3.0-m section of the string. The crests move at 20.0 m/s.
What is the shortest horizontal distance from a crest to a point of zero acceleration?
0.38m
0.75m
1.5m
3.0m
The correct Answer is:A
To solve the problem step by step, we can follow these instructions:
Step 1: Determine the wavelength (λ)
Given that there are 2 cycles in a 3.0 m section of the string, we can find the wavelength by dividing the total distance by the number of cycles.
Wavelength(λ)=Total distanceNumber of cycles=3.0m2=1.5m
Step 2: Understand the wave motion
The wave is a transverse wave, and the particles of the string undergo simple harmonic motion (SHM). The acceleration of a particle in SHM is given by the formula:
a=−ω2x
where x is the displacement from the mean position. The acceleration is zero when x=0, which corresponds to the mean position of the wave.
Step 3: Identify the distance from the crest to the mean position
In a sine wave, the distance from a crest to the mean position is one-quarter of the wavelength. Therefore, we can express this distance as:
Distance from crest to mean position=λ4
Step 4: Calculate the distance
Now that we know the wavelength λ=1.5m, we can calculate the distance from the crest to the point of zero acceleration:
D=λ4=1.5m4=0.375m
Step 5: Round the answer
Rounding the answer to two decimal places, we get:
D≈0.38m
Final Answer
The shortest horizontal distance from a crest to a point of zero acceleration is approximately 0.38 m.
---
Given that there are 2 cycles in a 3.0 m section of the string, we can find the wavelength by dividing the total distance by the number of cycles.
The wave is a transverse wave, and the particles of the string undergo simple harmonic motion (SHM). The acceleration of a particle in SHM is given by the formula:
In a sine wave, the distance from a crest to the mean position is one-quarter of the wavelength. Therefore, we can express this distance as:
Now that we know the wavelength λ=1.5m, we can calculate the distance from the crest to the point of zero acceleration:
Rounding the answer to two decimal places, we get:
The shortest horizontal distance from a crest to a point of zero acceleration is approximately 0.38 m.
Topper's Solved these Questions
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Matrix -Match)
Explore 7 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (More than One Coorect Choice Type)
Explore 10 Videos
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 5 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
Similar Questions
A harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90m/s2 respectively. Velocity of the wave is 20m/s. Find the waveform.
View SolutionA wave pulse on a string moves a distance of 8 min 0.05 s.
What would be the wavelength of the wave on the same string if its frequency is 200 Hz?
View Solution
Knowledge Check
A periodic transverse wave is established on a string such that there are exactly two cycles traveling along a 3.0-m section of the string. The crests move at 20.0 m/s.
What is the frequency of the wave?A0.67 HzB1.33 HzC13 Hz.D30 HzA periodic transverse wave is established on a string such that there are exactly two cycles traveling along a 3.0-m section of the string. The crests move at 20.0 m/s.
How could the speed of the wave be incresed?ABy increasing the periodBBy increasing the tension in the stringCBy decreasing the amplitudeDBy decreasing the frequencyA periodic transverse wave is established on a string such that there are exactly two cycles traveling along a 3.0-m section of the string. The crests move at 20.0 m/s.
How long does it take a particle at the top of a crest to reach the bottom of an adjacent trough?A0.018sB0.038sC0.075sD0.150s
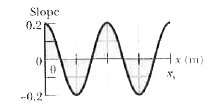
A sinusoidal wave travels along a string under tension. Figure 16-52 gives the slopes along the string at time t=0. The scale of the x axis is st by xs=0.40m What is the amplitude of the wave?
View SolutionA transverse wave travelling in a string produce maximum transverse velocity of 3m/s and maximum transverse acceleration 90m/s2 in a particle. If the velocity of wave in the string is 20m/s. Datermine the equation of the wave ?
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionA transverse wave described by equation y=0.02sin(x+30t) (where x and t are in meters and seconds, respectively) is travelling along a wire of area of cross-section 1mm2 and density 8000kg/m3. What is the tension in the string?
View SolutionA transverse periodic wave is established on a string. The wave is described by the expression
y=0.005sin(20.0x−2.4πft)
where y is in meters when x and t are in meters and seconds, respectively. If the wave travels with a speed of 20.0 m/s, what is its frequency: f?
View Solution