Here are the equations of three waves:
(1) (y) (x,t) =2 sin (4x-2t), (2). (y)(x,t) =sin (3x-4t), (3) (y) (x,t)=2 sin (3x-3t). Rank the waves according to their (a) wave speed and (b) maximum speed perpendicular to the wave's direction of travel (the transverse speed), greatest first.
The correct Answer is:(a) 2,3,1; (b) 3 then 2 and 1 tie (find amplitude of dy/dt)
To solve the problem, we need to analyze the given wave equations and find the wave speed and the maximum transverse speed for each wave. Let's break it down step by step.
Step 1: Identify the wave equations
The given wave equations are:
1. y1(x,t)=2sin(4x−2t)
2. y2(x,t)=sin(3x−4t)
3. y3(x,t)=2sin(3x−3t)
Step 2: Extract parameters from the wave equations
From the general wave equation y(x,t)=Asin(kx−ωt), we can identify:
- Amplitude A
- Wave number k
- Angular frequency ω
For each wave:
- For wave 1: A1=2,k1=4,ω1=2
- For wave 2: A2=1,k2=3,ω2=4
- For wave 3: A3=2,k3=3,ω3=3
Step 3: Calculate wave speed
The wave speed v can be calculated using the formula:
v=ωk
Calculating for each wave:
1. For wave 1:
v1=ω1k1=24=0.5
2. For wave 2:
v2=ω2k2=43≈1.33
3. For wave 3:
v3=ω3k3=33=1
Step 4: Rank the waves according to wave speed
From the calculated speeds:
- v2≈1.33 (wave 2)
- v3=1 (wave 3)
- v1=0.5 (wave 1)
Ranking according to wave speed:
1. Wave 2
2. Wave 3
3. Wave 1
Step 5: Calculate maximum transverse speed
The maximum transverse speed vt can be calculated using:
vt=A⋅ω
Calculating for each wave:
1. For wave 1:
vt1=A1⋅ω1=2⋅2=4
2. For wave 2:
vt2=A2⋅ω2=1⋅4=4
3. For wave 3:
vt3=A3⋅ω3=2⋅3=6
Step 6: Rank the waves according to maximum transverse speed
From the calculated transverse speeds:
- vt3=6 (wave 3)
- vt1=4 (wave 1)
- vt2=4 (wave 2)
Ranking according to maximum transverse speed:
1. Wave 3
2. Wave 1 and Wave 2 (equal)
Final Answers
(a) Ranking according to wave speed:
1. Wave 2
2. Wave 3
3. Wave 1
(b) Ranking according to maximum transverse speed:
1. Wave 3
2. Wave 1 and Wave 2 (equal)
The given wave equations are:
1. y1(x,t)=2sin(4x−2t)
2. y2(x,t)=sin(3x−4t)
3. y3(x,t)=2sin(3x−3t)
From the general wave equation y(x,t)=Asin(kx−ωt), we can identify:
- Amplitude A
- Wave number k
- Angular frequency ω
- For wave 1: A1=2,k1=4,ω1=2
- For wave 2: A2=1,k2=3,ω2=4
- For wave 3: A3=2,k3=3,ω3=3
The wave speed v can be calculated using the formula:
v=ωk
1. For wave 1:
v1=ω1k1=24=0.5
2. For wave 2:
v2=ω2k2=43≈1.33
3. For wave 3:
v3=ω3k3=33=1
From the calculated speeds:
- v2≈1.33 (wave 2)
- v3=1 (wave 3)
- v1=0.5 (wave 1)
1. Wave 2
2. Wave 3
3. Wave 1
The maximum transverse speed vt can be calculated using:
vt=A⋅ω
1. For wave 1:
vt1=A1⋅ω1=2⋅2=4
2. For wave 2:
vt2=A2⋅ω2=1⋅4=4
3. For wave 3:
vt3=A3⋅ω3=2⋅3=6
From the calculated transverse speeds:
- vt3=6 (wave 3)
- vt1=4 (wave 1)
- vt2=4 (wave 2)
1. Wave 3
2. Wave 1 and Wave 2 (equal)
(a) Ranking according to wave speed:
1. Wave 2
2. Wave 3
3. Wave 1
1. Wave 3
2. Wave 1 and Wave 2 (equal)
Topper's Solved these Questions
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Problems
Explore 60 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Single Correct Choice Type)
Explore 33 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 5 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
Similar Questions
Two waves with the same amplitude and wavelength interface in three different situation to produce resultant waves with the following equations:
(1) y' (x,t) =4 sin (5x-4t)
(2) y' (x,t) =4 sin (5x) cos (4t)
(3) y' (x,t) =4 sin (5x+4t)
In which stituation are the two combing waves traveling (a) toward positive x, (b) toward negative x, and (c) in opposite directions?
View SolutionIf the equation of a travelling wave is given as y=40cos(1600t+6x), (where y is in millimeter, t is in second and x is in meter), then ratio of the wave speed to the maximum particle speed will be
View Solution
Knowledge Check
The mathmaticaly form of three travelling waves are given by
Y1=(2cm)sin(3x−6t)
Y2=(3cm)sin(4x−12t)
And Y3=94cm)sin(5x−11t)
of these waves,AWave 1 has greatest wave speed and greatest maximum transverse string speedBwave 2 has greatest wave speed and wave 1 has greatest maximum transverse string speedCwave 3 has greatest wave speed and wave 1 has greatest maximum transverse string speedDwave 2 has greatest wave speed and wave 3 has greatest maximum transverse string speedThe equation y=4+2sin(6t−3x) represents a wave motion. Then, wave speed and amplitude, respectively are
Awave speed 1 unit, amplitude 6 unitBwave speed 2 unit, amplitude 2 unitCwave speed 4 unit, amplitude 1/2 unitDwave speed 1/2 unit, amplitude 5 unitThe equation of a wave is given by y=2sin(314t−2x+π/2) m, the wave length of the wave is
A2.0 mB1.57 mC6.28 mD3.14 m
Use the wave equation to find the speed of a wave given by y(x,t)=(3.00mm)sin[(3.00m−1)x−(8.00s−1)t]).
View SolutionWhen two progressive waves y1=4sin(2x−6t) and y2=3sin(2x−6t−π2) are superimposed, the amplitude of the resultant wave is
View SolutionThe equation of progressive wave is y=0.2sin2π[t0.01−x0.3], where x and y are in metre and t is in second. The velocity of propagation of the wave is
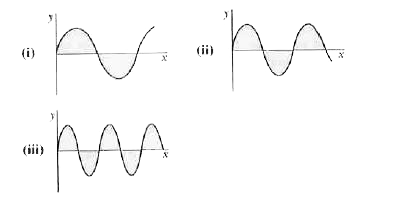
View SolutionThree traveling sinusoidal waves are on identical strings. with the same tension. The mathematical forms of the waves are y1(x,t)=ymsin(3x−6t),y2(x,t)=ymsin(4x−8t),andy3(x,t)sin(6x−12t), where x is in meters and t is in seconds. Match each mathematical form to the appropriate graph below:
View SolutionThe equation of a transverse wave is given by y=20sinπ(4t−0.04x) where x and y are in m and t is in sec. The frequency of the wave is
View Solution

