Two charges +8q and -2q are fixed on X-axis at origin and x=+a locations. A third charge +q is to be located on X-axis (other than infinitely far away) so that it is in equilibrium. The location of the third charge is correctly represented by
KEY IDEA
If →F1 is the force on the proton due to charge q1 and →F1 is the force on the proton due to charge q2, then the point we seek is where Thus, →F1+→F2=0. Thus,
→F1=−→F2 (22−8)
This tells us that at the point we seek, the forces acting on the proton due to the other two particles must be of equal magnitudes
→F1=→F2, (22−9)
and that the forces must have opposite directions.
Reasoning : Because a proton has a positive charge, the proton and the particle of charge q1 are of the same sign, and force →F1 on the proton must point away from q1. Also, the proton and the particle of charge q2 are of opposite signs, so force →F2 on the proton must point toward q2. "Away from q1" and "toward q2" can be in opposite directions only if the proton is located on the x axis.
If the proton is on the x axis at any point between q1 and q2, such as point P in Fig. 22-9b, then →F1and→F2 are in the same direction and not in opposite directions as required. If the proton is at any point on the x axis to the left of q1, such as point S in Fig. 22-9c, then →F1 and →F2 are in opposite directions. However, Eq. 22-4 tells us that →F1and→F2 cannot have equal magnituded there: F1 must be greater than F2, because F1 is produced by a closer charge (with lesser r) of greater magnitude (8q versus 2q).
Finally, if the proton is at any point on the x axis to the right of q2, such as point R in Fig. 22-9d, then →F1and→F2 are again in opposite directions. However, because now
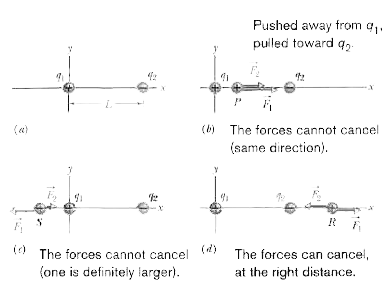
the charge of greater magnitude (q1) is farther away from the proton than the charge of lesser magnitude, there is a point at which F1 is equal to F2. Let x be the coordinate of this point, and let qp be the charge of the proton.
Calculations: With Eq. 22-4, we can now rewrite Eq. 22-9:
14πε08qqpx2=14πε02qq0(x−L)2. (22−10)
Rearranging Eq. 22-10 gives us
(x−Lx)2=14
After taking the square roots of both sides, we find
x−Lx=12
and x = 2L. (Answer)
The equilibrium at x = 2L is unstable, that is, if the proton is displaced leftward from point R, then F1andF2 both increase but F2 increases more (because q2 is closer than q1), and a net force will drive the proton farther leftward. If the proton is displaced reightward, both F1andF2 decrease but F2 decrease more, and a net force will then drive the protonfarther rightward. In a stable equilibrium, if the proton is displaced slightly, it returns to the equilibrium position.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
Two free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then magnitude of third charge and postion,
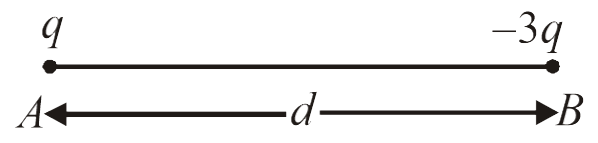
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
View Solution
Knowledge Check
Two point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
AAt a distance L3 from +4q charge, 4q9BAt a distance L3 from +4q charge −4q9CAt a distance 2L3 from +4q charge −4q9DAt a distance 2L3 from +q charge 4q9Two force point charges +q and +4q are a distance l apart. A third charge q1 is so placed that the entire system is in equilibrium. Find the location, magnitude and sign of the third charge.
Aq1=49qBq1=−49qCq1 is to be placed at a distance l/3 from q.Dq1 is to be placed at a distance 2l3 from 4q.Two point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
Auknknown charge is −4q/9Bunknown charge is −9q/4Cit should be at (x/3)from smaller chargge between themDnone of these
Two point electric charges of value q and 2q are kept at a distance d apart from each other in air. A third charge Q is to be kept along the same line in such a way that the net force action on q and 2q is zero. Calculate the position of charge Q in terms of q and d.
View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?

View SolutionTwo free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then
View SolutionTwo charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
View Solution
