(a). It is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y(_o) ltb rgt where po=1.25kgm−3 is the density at sea level, and yo is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant
(b). A large He balloon of volume 1425m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[take yo=8000mandρHe=0.18kgm−3]Solution in Tamil
8km, If we consider the variation of g with altitude the height is somewhat more. About 8.2km.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS Book:NCERT TAMILChapter:MECHANICAL PROPERTIES OF FLUIDS Exercise:EXERCISE
Explore 45 Videos
- LAWS OF MOTIONBook:NCERT TAMILChapter:LAWS OF MOTIONExercise:EXERCISE (V. Numerical Problems)
Explore 14 Videos
- MECHANICAL PROPERTIES OF SOLIDS Book:NCERT TAMILChapter:MECHANICAL PROPERTIES OF SOLIDS Exercise:Exercises
Explore 21 Videos
Similar Questions
Why the blood pressure in humans is greater at the feet than at the brain?
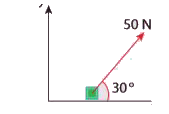
View SolutionA force of 50N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions
View SolutionA steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 1x10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
View Solution(a) It is known that density rho of air decrease with height y(in metres ) as rho =rho_(0)e^(-y//y_(0)) where rho_(0)=1.25kgm^(-3) is the density at see level , and y_(0) is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmospere remians a constant (isothermal conditions). Also assume that the value of g remains constant. (b) A large He balloon of volume 1425m^(3) is used to lift a payload of 400g . Assume that the balloon maintains constant radius as it rises. How high does it rise? [take y_(0)=800m and rho_(He) = 0.18kg//m^(3) ].
View SolutionThe density of air in atomsphere decreases with height and can be expressed by the relation. rho=rho_(0)e^(-Ah) Where rho_(0) is the density at sea-level, A is a constant and h is the height. Calculate the atmospheric pressure at sea -level. assume g to be constant.
View Solution(a). It is known that density rho of air decreases with height y as rho=rho_(0)e^(-y//y(_o)) ltb rgt where p_(o)=1.25kgm^(-3) is the density at sea level, and y_(o) is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant (b). A large He balloon of volume 1425m^(3) is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise? [take y_(o)=8000m and rho_(He)=0.18kgm^(-3) ]
View SolutionAssuming that the atmosphere has the same density anywhere as at sea level (ρ=1.3kgm−3) and g to be constant (g=10ms−2). What should be the approximate height of atmosphere ?
(ρ0=1.01×105Nm−2)
View Solutionयह ज्ञात है, की वायु का घनत्व ρ ऊँचाई y ( मीटरों में ) के साथ इस सम्बन्ध के अनुसार घटता है -
ρ=ρ0e−y/y0 ,
यहाँ समुद्र तल पर वायु का घनत्व ρ0=1.25kgm−3 तथा y0 एक नियतांक है | घनत्व में इस परिवर्तन को वायुमंडल का नियम कहते है | यह संकल्पना करते हुए की वायुमंडल का ताप नियत रहता है ( समतापी अवस्था ) इस नियम को प्राप्त कीजिए | यह भी मानिए की g मान नियत रहता है |
View SolutionThe density of air at one atmospheric pressure is 0.9kgm−3 What will be its density at "4" atmospheric pressure,when temperature remains constant?
View Solution(a) हम जानते है की वायु के घनत्व ρ ऊँचाई y (मीटरो में ) के साथ इस संबंध के अनुसार घटता है:
ρ=ρ0e−y/yo
यहाँ समुद्र तल पर वायु का घनत्व ρo=1.25kgm−3 तथा yo एक नियतांक है। घनत्व में इस परिवर्तन को वायुमंडल का नियम कहते है। यह संकल्पना करते हुए कि वायुमंडल का ताप नियत रहता है। (समतापी अवस्था) इस नियम को प्राप्त कीजिए। यह भी मानिए की g का मान नियत रहता है।
(b) 1425m3 आयतन का हीलियम से भरा कोई बड़ा गुब्बारा 400kg के किसी पेलोड को उठाने के काम में लाया जाता है। यह मानते हुए कि ऊपर उठते समय गुब्बारे की त्रिज्या नियत रहती है, गुब्बारा कितनी अधिकतम ऊँचाई तक ऊपर उठेगा?
[yo=8000m तथा ρHe=0.18kgm−3 लीजिए।
View SolutionIt is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y0
where ρ0=1.25kgm−3 is the density at sea level. And y0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
A large He balloon of volume 1425m3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View SolutionIt is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y0
where ρ0=1.25kgm−3 is the density at sea level. And y0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
A large He balloon of volume 1425m3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View SolutionIt is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y0
where ρ0=1.25kgm−3 is the density at sea level. And y0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
A large He balloon of volume 1425m3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View SolutionIt is known that density rho of air decreases with height y as rho=rho_0e^(-y//y_0) where rho_0=1.25 kg m^-3 is the density at sea level. And y_0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant. A large He balloon of volume 1425 m^3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View Solution(a). It is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y(_o) ltb rgt where po=1.25kgm−3 is the density at sea level, and yo is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant
(b). A large He balloon of volume 1425m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[take yo=8000mandρHe=0.18kgm−3]
View SolutionIt is known that density rho of air decreases with height y as -y//y_(0) rho=rho_(o)e where rho_(o)=1.25kgm^(-3) is the density at sea level and y_(o) is a constant . This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions).Also assume that the value of g remains constant. (b) A large He balloon of volume 1425m^(3) is used to lift a payload of 400 kg . Assume that the balloon maintains constant radius as it rises . How high does it rise ? (y_(o)=8000mandrho_(He)=0.18kgm^(-3)) .
View Solution