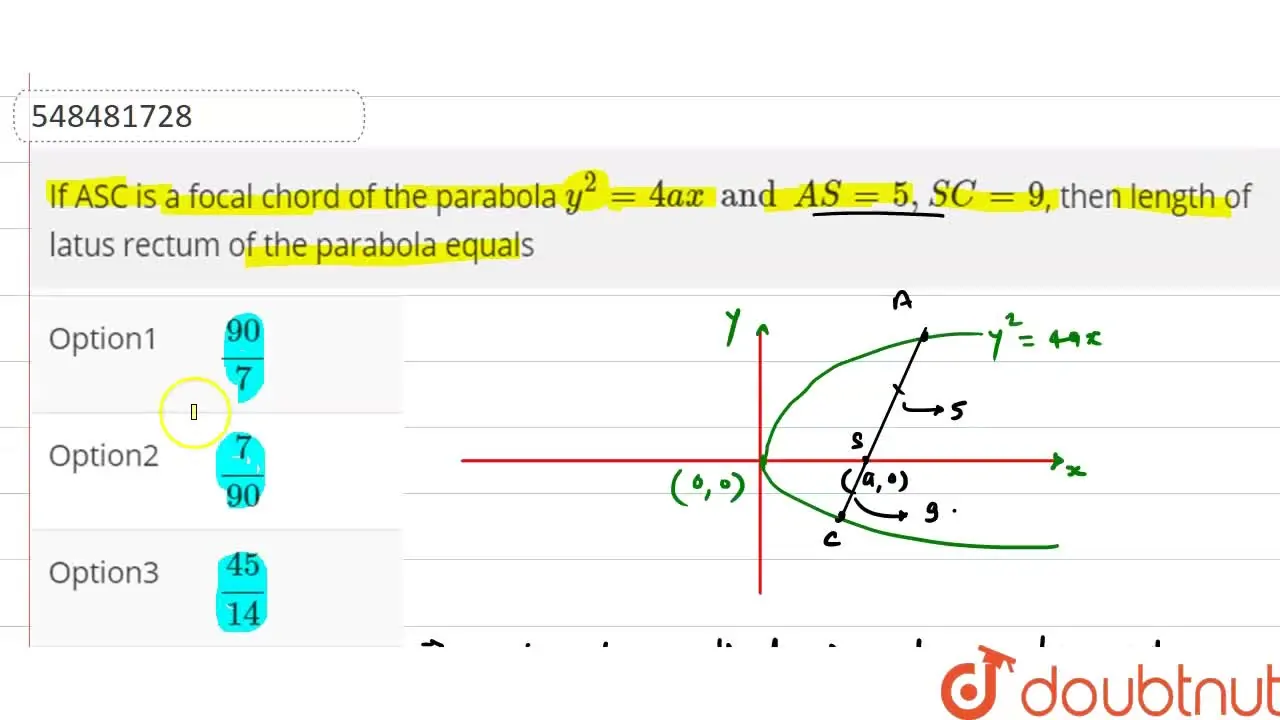
If ASC is a focal chord of the parabola $y^{2} = 4 a x and A S = 5, S C = 9$ , then length of latus rectum of the parabola equals

A

$\frac{90}{7}$

B

$\frac{7}{90}$

C

$\frac{45}{14}$

D

$\frac{14}{45}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

|

Answer

Step by step video, text & image solution for If ASC is a focal chord of the parabola y^(2)=4ax and AS=5,SC=9, then length of latus rectum of the parabola equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS CONIC SECTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The length of the latus rectum of the parabola $y^{2} = 8 x$ is
A4
B6
C8
D10
Question 2 - Select One
If AFB is a focal chord of the parabola $y^{2} = 4 a x$ such that $A F = 4$ and $F B = 5$ then the latus-rectum of the parabola is equal to
A80
B $\frac{9}{80}$
C9
D $\frac{80}{9}$
Question 3 - Select One
The length of the latus rectum of the parabola $x^{2} = - 28 y$ is
A28 units
B7 units
C14 units
D21 units

MTG-WBJEE-CONIC SECTIONS-WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3 : One or More than One Option Correct Type)

Home
Ask Doubt
Profile