In addition to the basic typing keys, desktop and notebook computer keyboards include a(n)______keypad to efficiently move the screen-based insertion point.
editing
number
locked
docked
The correct Answer is:B
Step by step video, text & image solution for In addition to the basic typing keys, desktop and notebook computer keyboards include a(n)______keypad to efficiently move the screen-based insertion point. by General Knowledge experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a ideal crystal there nust be regular repeating arrangement of the constuting particles and its entropy must be zero at absolute zero at absolute zero temperature. However, it is impossible to obtain an ideal crystal and it suffers from certain defects called imperfections. In pure crystal these defects arise either due to disorder or dislocation of the movement of the particles even at absolute zero temperature. Such defect increases with rise in temperature. In addition ti this, certain defects arise due to the pressure of some impurities. Such defects not only modify the existing properties of the crystalline solid but also impart certain new characteritics to them.
In pure crystal, e.g, silicon or germanium at 0K, the electrons are prsent in fully occupied lowest energy states and are not xpected to conduct any electricity. However at temperature above 0K, some electron leave their bonds and become free to move in the crystal lattice, giving rise to and become free to move in the crystal lattice, giving rise to electrical conductivity. The electron deficient bonds, called holes (+vely charged) and thermally mobile electrons move in opposite direction under the electric field.
Stoichiometric ppoint defects include (a) Schottky defects, which arise due to missing of both cations and anions from their lattice sites without disturbing the stoichiometry and
(b) Frenked defects, which arise due to misplacement of certian ions in the crystal lattice. The former defect gives rise to no change of density.
Another type of defects are non-stoichometry defects where the cetions and anion are not present in the stoichiometry ratio. In metal excess defect, metal ions or positive ions are in excess as compared to anions of non-metals stoichiometrycally. On the other hand in metal deficiency defect, the cations are in lesser proportion than stoichiometric value. Since the crystal is neutral electrically, the balance of charge is maintained by free electrons or extra positive charges. The metal excess defects gives rise to conduction of electricity due to the presence of free electrons. Also crystals having metal excess defects are paramagnetic and coloured due to the presence of electrons in the anion vacancies.
Impurity defects arise when some foreign atoms are present at the lattice sites in place of the host atoms or at the vacant interstitial sites.
When 15 group elements like P or are doped into Si or Ge, the added impurity atoms occupy the lattice sites forming four covalent bonds with 4 Si/Ge atoms leaving an extra electron free to move. Such a crystal is said to be n-type semi conductor because the conduction of electricity is due to movement of extra unbounded electrons.
If doping of a covalent crystal of 14 group elements are caused by addition of small amounts of elements are caused by addition of small amounts of elements of group 13, e.g, Al or Ga with three valence electrons, one covalent bond formed will be electron deficient and acts as a positive hole. The presence of such holes in the crystal leads to electrical conductivity and the the crystal is said to be p-type semiconductor.
In the crystal of Fe0.93 O, the percentage of Fe(III) will be:
View SolutionIn a ideal crystal there nust be regular repeating arrangement of the constuting particles and its entropy must be zero at absolute zero at absolute zero temperature. However, it is impossible to obtain an ideal crystal and it suffers from certain defects called imperfections. In pure crystal these defects arise either due to disorder or dislocation of the movement of the particles even at absolute zero temperature. Such defect increases with rise in temperature. In addition ti this, certain defects arise due to the pressure of some impurities. Such defects not only modify the existing properties of the crystalline solid but also impart certain new characteritics to them.
In pure crystal, e.g, silicon or germanium at 0K, the electrons are prsent in fully occupied lowest energy states and are not xpected to conduct any electricity. However at temperature above 0K, some electron leave their bonds and become free to move in the crystal lattice, giving rise to and become free to move in the crystal lattice, giving rise to electrical conductivity. The electron deficient bonds, called holes (+vely charged) and thermally mobile electrons move in opposite direction under the electric field.
Stoichiometric ppoint defects include (a) Schottky defects, which arise due to missing of both cations and anions from their lattice sites without disturbing the stoichiometry and
(b) Frenked defects, which arise due to misplacement of certian ions in the crystal lattice. The former defect gives rise to no change of density.
Another type of defects are non-stoichometry defects where the cetions and anion are not present in the stoichiometry ratio. In metal excess defect, metal ions or positive ions are in excess as compared to anions of non-metals stoichiometrycally. On the other hand in metal deficiency defect, the cations are in lesser proportion than stoichiometric value. Since the crystal is neutral electrically, the balance of charge is maintained by free electrons or extra positive charges. The metal excess defects gives rise to conduction of electricity due to the presence of free electrons. Also crystals having metal excess defects are paramagnetic and coloured due to the presence of electrons in the anion vacancies.
Impurity defects arise when some foreign atoms are present at the lattice sites in place of the host atoms or at the vacant interstitial sites.
When 15 group elements like P or are doped into Si or Ge, the added impurity atoms occupy the lattice sites forming four covalent bonds with 4 Si/Ge atoms leaving an extra electron free to move. Such a crystal is said to be n-type semi conductor because the conduction of electricity is due to movement of extra unbounded electrons.
If doping of a covalent crystal of 14 group elements are caused by addition of small amounts of elements are caused by addition of small amounts of elements of group 13, e.g, Al or Ga with three valence electrons, one covalent bond formed will be electron deficient and acts as a positive hole. The presence of such holes in the crystal leads to electrical conductivity and the the crystal is said to be p-type semiconductor.
The type of semiconduction shown by crystal capable of showing Schottky defect, will be :
View Solution
Knowledge Check
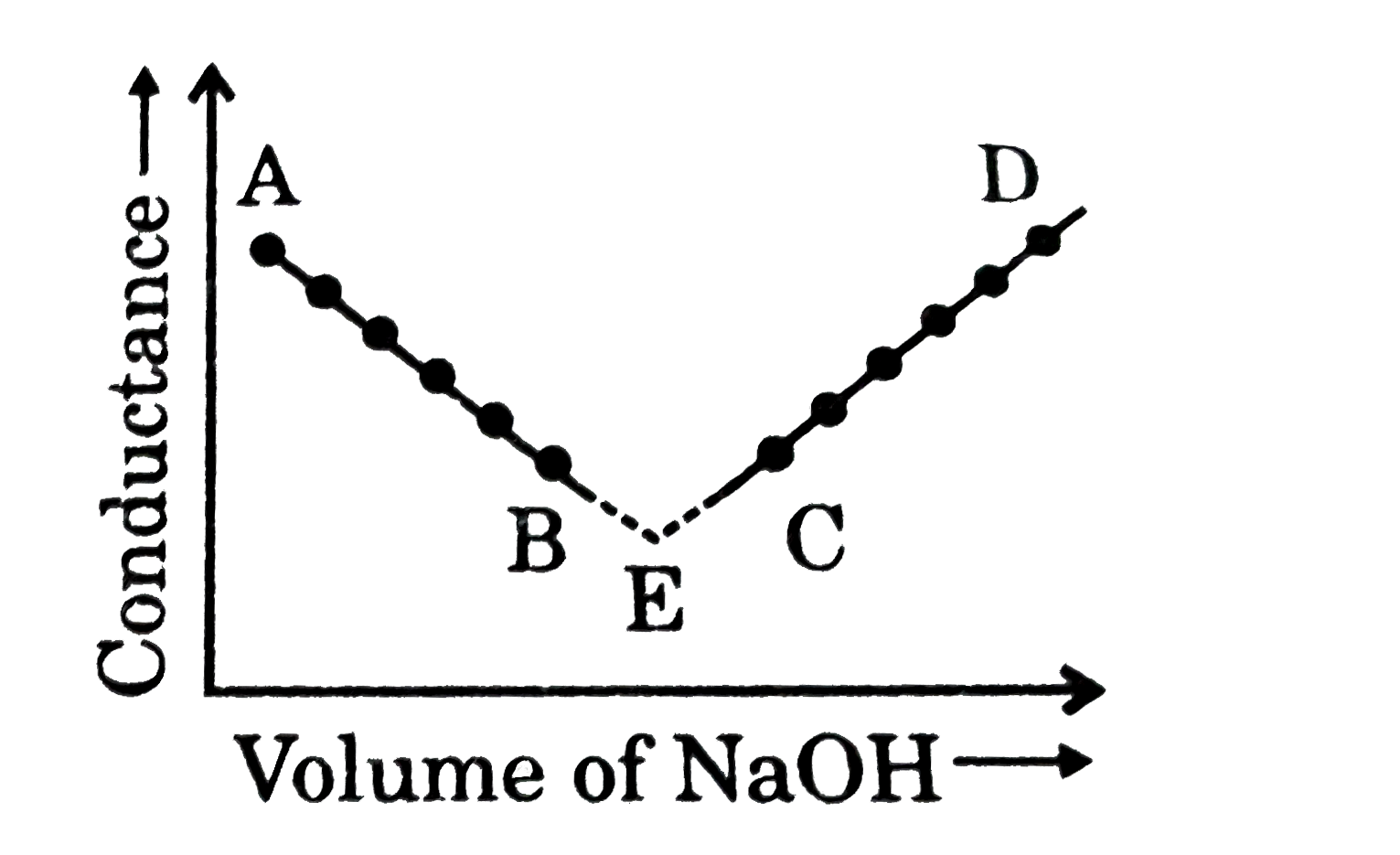
The principle on conductometric titration is based in the fact that during the titration, one of the ions is replaced by the other and invariably thses two ions differ in the ionic conductivity with the result that the conductivity of the solution varies during the course of the titration.Take,for example,the titration between strong acid, say HCl. and a strong base, say NaOH.Before NaOH is added the conuctance of HCl solution has a high value due ti the persence if highly hydrogen ions.As NaOH is added,H+ ions are the replaced by relatively slower moving Na+ ions.Consequently, the conductance of the solution decrease and this continues right upto the enuivalence point where the solution contains only NaCL.Beyond the equivalence point if more of NaOH is added, then the solution contains an excess of the fast moving OH− with the result that its as more of NaoH added, we plot the conductance value vs the amount of NaOH added we get curve of the type shown in figure.The descending portion AB represents the conductance before the equivalence point (solution cintains a mixture if acid HCl and the salt NaCL and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCL and the excess of NaOH). The point E which repersents only the minimum conductance is alkali and thus repersents the equivalence point.This point can, however, be obtained by the extrapoltion of the lines AB and CD and therefore one is not very particular in location this point experimentally as it is in the case of ordinary acid -base involving the acid base indicators

LET us take the specific exaanple of acetic acid being titration against NaOH.Before the addition the of alkali, the solution shows poor conductance due to feeble inization of acetic acid.Initially the addtion of alkali causes not only the replacement of H+ by Na+ but also suppresses the thus the conductance of the solution decrease in the begnning .But very soon the conductance starts increasing as addetion NaOH thus causing neutralizes the undissociated HAc to HAc with strong condutance eletroyte Na+Ac−.The increase in conducting OH− ions gtthe graph near the highly equivalence point actual equivalence point can as usual be ontained by the extrapoiation method
In all thses graphs it been assumed that the vloume change due addition of solution from burette in negligible heane vloume change of the sloution in beaker the conuctance of which is measured is almost constant throughout the measurement
the nature of curve obtained for the titration between weak acid vs strong base as described in the above will beA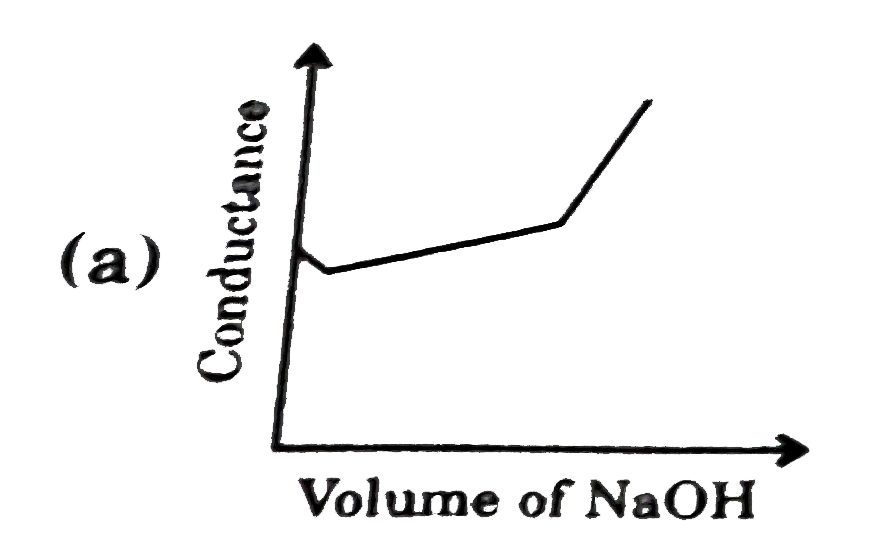 B
B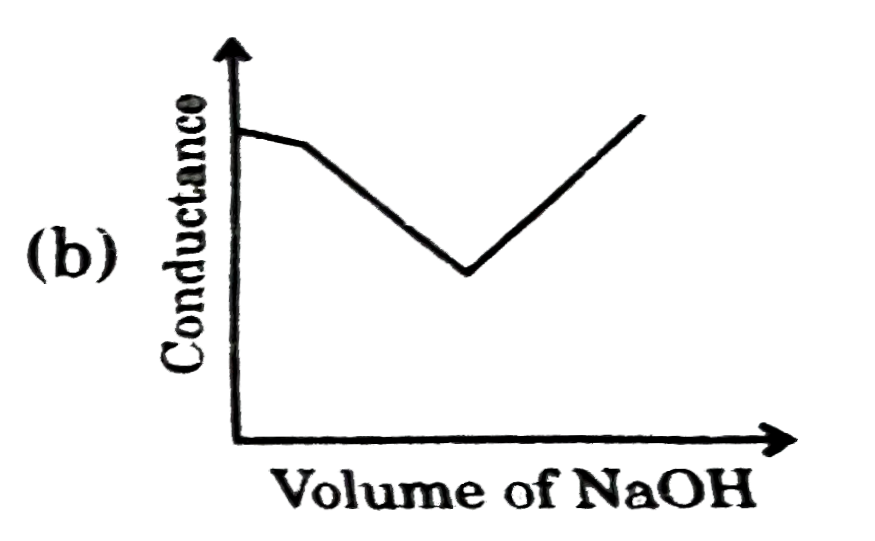 C
C D
D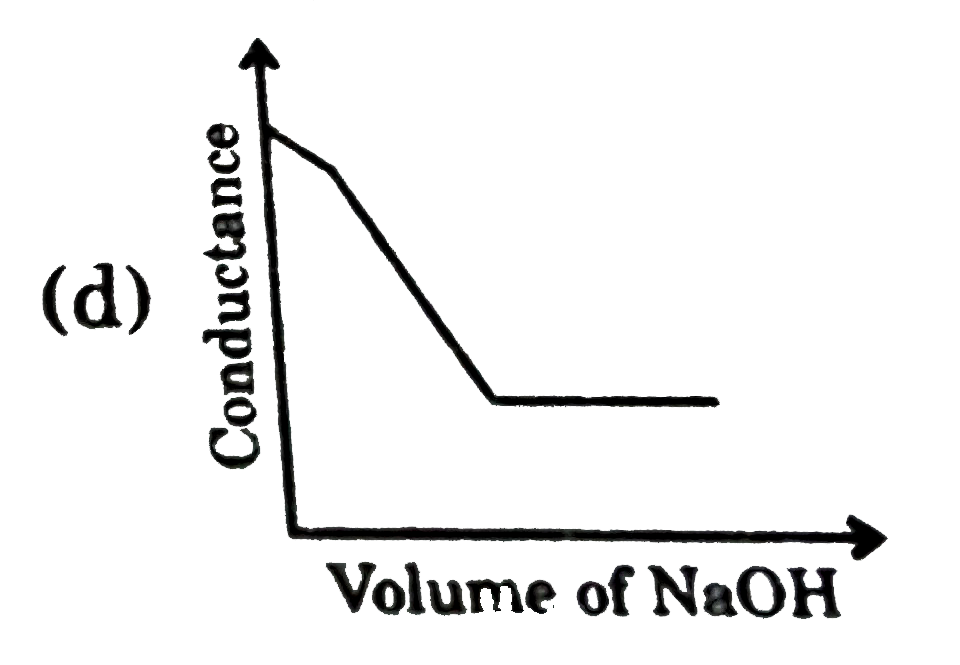
The principle on conductometric titration is based in the fact that during the titration, one of the ions is replaced by the other and invariably thses two ions differ in the ionic conductivity with the result that the conductivity of the solution varies during the course of the titration.Take,for example,the titration between strong acid, say HCl. and a strong base, say NaOH.Before NaOH is added the conuctance of HCl solution has a high value due ti the persence if highly hydrogen ions.As NaOH is added,H+ ions are the replaced by relatively slower moving Na+ ions.Consequently, the conductance of the solution decrease and this continues right upto the enuivalence point where the solution contains only NaCL.Beyond the equivalence point if more of NaOH is added, then the solution contains an excess of the fast moving OH− with the result that its as more of NaoH added, we plot the conductance value vs the amount of NaOH added we get curve of the type shown in figure.The descending portion AB represents the conductance before the equivalence point (solution cintains a mixture if acid HCl and the salt NaCL and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCL and the excess of NaOH). The point E which repersents only the minimum conductance is alkali and thus repersents the equivalence point.This point can, however, be obtained by the extrapoltion of the lines AB and CD and therefore one is not very particular in location this point experimentally as it is in the case of ordinary acid -base involving the acid base indicators
LET us take the specific exaanple of acetic acid being titration against NaOH.Before the addition the of alkali, the solution shows poor conductance due to feeble inization of acetic acid.Initially the addtion of alkali causes not only the replacement of H+ by Na+ but also suppresses the thus the conductance of the solution decrease in the begnning .But very soon the conductance starts increasing as addetion NaOH thus causing neutralizes the undissociated HAc to HAc with strong condutance eletroyte Na+Ac−.The increase in conducting OH− ions gtthe graph near the highly equivalence point actual equivalence point can as usual be ontained by the extrapoiation method
In all thses graphs it been assumed that the vloume change due addition of solution from burette in negligible heane vloume change of the sloution in beaker the conuctance of which is measured is almost constant throughout the measurement
If a 100 ml solution of 0.1 MHBr is titration using a very concentrated solution of NaOH then the conductivity (specific conductance0 of this solution at the equivalence wil be (assume volume change is negligible due addition of NaOH). Report your answer after mulitiplying it with 100 inSm−1
[Given : λ∘(Na+)=8×10−3Sm2mol−1,λ∘(Br−)=4×10−3Sm2mol−1]A6B12C15D24The principle on conductometric titration is based in the fact that during the titration, one of the ions is replaced by the other and invariably thses two ions differ in the ionic conductivity with the result that the conductivity of the solution varies during the course of the titration.Take,for example,the titration between strong acid, say HCl. and a strong base, say NaOH.Before NaOH is added the conuctance of HCl solution has a high value due ti the persence if highly hydrogen ions.As NaOH is added,H+ ions are the replaced by relatively slower moving Na+ ions.Consequently, the conductance of the solution decrease and this continues right upto the enuivalence point where the solution contains only NaCL.Beyond the equivalence point if more of NaOH is added, then the solution contains an excess of the fast moving OH− with the result that its as more of NaoH added, we plot the conductance value vs the amount of NaOH added we get curve of the type shown in figure.The descending portion AB represents the conductance before the equivalence point (solution cintains a mixture if acid HCl and the salt NaCL and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCL and the excess of NaOH). The point E which repersents only the minimum conductance is alkali and thus repersents the equivalence point.This point can, however, be obtained by the extrapoltion of the lines AB and CD and therefore one is not very particular in location this point experimentally as it is in the case of ordinary acid -base involving the acid base indicators

LET us take the specific exaanple of acetic acid being titration against NaOH.Before the addition the of alkali, the solution shows poor conductance due to feeble inization of acetic acid.Initially the addtion of alkali causes not only the replacement of H+ by Na+ but also suppresses the thus the conductance of the solution decrease in the begnning .But very soon the conductance starts increasing as addetion NaOH thus causing neutralizes the undissociated HAc to HAc with strong condutance eletroyte Na+Ac−.The increase in conducting OH− ions gtthe graph near the highly equivalence point actual equivalence point can as usual be ontained by the extrapoiation method
In all thses graphs it been assumed that the vloume change due addition of solution from burette in negligible heane vloume change of the sloution in beaker the conuctance of which is measured is almost constant throughout the measurement
The most appropriate titration curve ibtained when a mixture of a strong acid (say HCl) and a weak acid (sayCH3COOH0 is titration with (say NaOH) will beA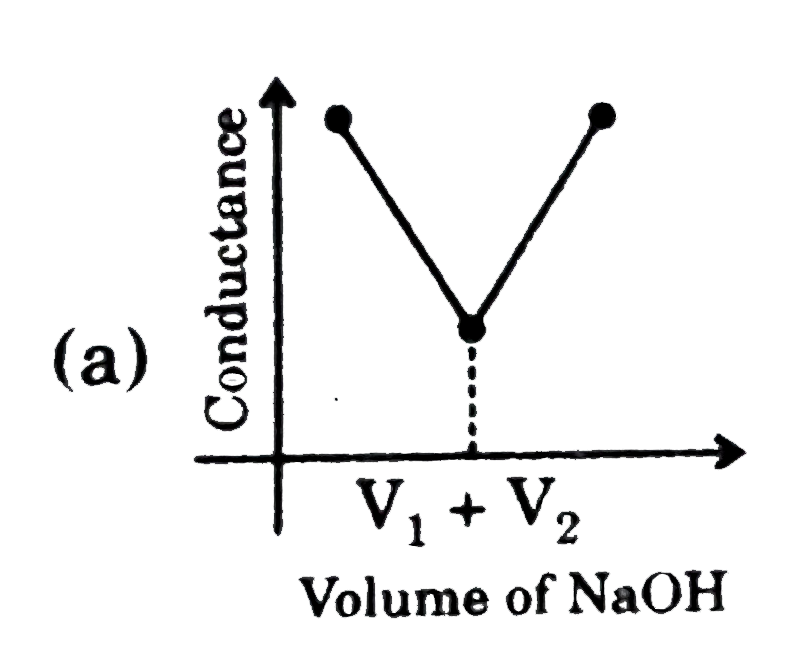 B
B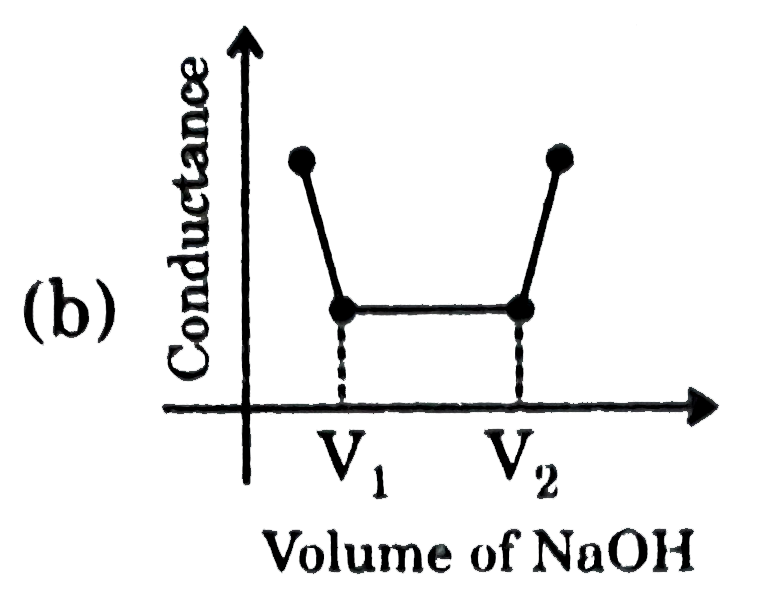 C
C D
D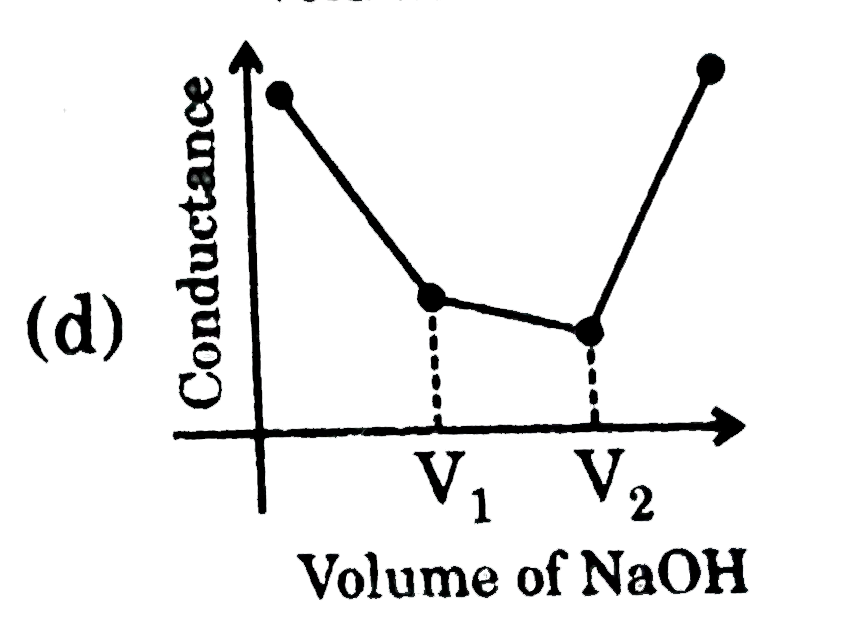
In a ideal crystal there nust be regular repeating arrangement of the constuting particles and its entropy must be zero at absolute zero at absolute zero temperature. However, it is impossible to obtain an ideal crystal and it suffers from certain defects called imperfections. In pure crystal these defects arise either due to disorder or dislocation of the movement of the particles even at absolute zero temperature. Such defect increases with rise in temperature. In addition ti this, certain defects arise due to the pressure of some impurities. Such defects not only modify the existing properties of the crystalline solid but also impart certain new characteritics to them.
In pure crystal, e.g, silicon or germanium at 0K, the electrons are prsent in fully occupied lowest energy states and are not xpected to conduct any electricity. However at temperature above 0K, some electron leave their bonds and become free to move in the crystal lattice, giving rise to and become free to move in the crystal lattice, giving rise to electrical conductivity. The electron deficient bonds, called holes (+vely charged) and thermally mobile electrons move in opposite direction under the electric field.
Stoichiometric ppoint defects include (a) Schottky defects, which arise due to missing of both cations and anions from their lattice sites without disturbing the stoichiometry and
(b) Frenked defects, which arise due to misplacement of certian ions in the crystal lattice. The former defect gives rise to no change of density.
Another type of defects are non-stoichometry defects where the cetions and anion are not present in the stoichiometry ratio. In metal excess defect, metal ions or positive ions are in excess as compared to anions of non-metals stoichiometrycally. On the other hand in metal deficiency defect, the cations are in lesser proportion than stoichiometric value. Since the crystal is neutral electrically, the balance of charge is maintained by free electrons or extra positive charges. The metal excess defects gives rise to conduction of electricity due to the presence of free electrons. Also crystals having metal excess defects are paramagnetic and coloured due to the presence of electrons in the anion vacancies.
Impurity defects arise when some foreign atoms are present at the lattice sites in place of the host atoms or at the vacant interstitial sites.
When 15 group elements like P or are doped into Si or Ge, the added impurity atoms occupy the lattice sites forming four covalent bonds with 4 Si/Ge atoms leaving an extra electron free to move. Such a crystal is said to be n-type semi conductor because the conduction of electricity is due to movement of extra unbounded electrons.
If doping of a covalent crystal of 14 group elements are caused by addition of small amounts of elements are caused by addition of small amounts of elements of group 13, e.g, Al or Ga with three valence electrons, one covalent bond formed will be electron deficient and acts as a positive hole. The presence of such holes in the crystal leads to electrical conductivity and the the crystal is said to be p-type semiconductor.
Which of the following statements is correct about the conduction of electricity in pure crystal of silicon at room temperature?
View SolutionIn a ideal crystal there nust be regular repeating arrangement of the constuting particles and its entropy must be zero at absolute zero at absolute zero temperature. However, it is impossible to obtain an ideal crystal and it suffers from certain defects called imperfections. In pure crystal these defects arise either due to disorder or dislocation of the movement of the particles even at absolute zero temperature. Such defect increases with rise in temperature. In addition ti this, certain defects arise due to the pressure of some impurities. Such defects not only modify the existing properties of the crystalline solid but also impart certain new characteritics to them.
In pure crystal, e.g, silicon or germanium at 0K, the electrons are prsent in fully occupied lowest energy states and are not xpected to conduct any electricity. However at temperature above 0K, some electron leave their bonds and become free to move in the crystal lattice, giving rise to and become free to move in the crystal lattice, giving rise to electrical conductivity. The electron deficient bonds, called holes (+vely charged) and thermally mobile electrons move in opposite direction under the electric field.
Stoichiometric ppoint defects include (a) Schottky defects, which arise due to missing of both cations and anions from their lattice sites without disturbing the stoichiometry and
(b) Frenked defects, which arise due to misplacement of certian ions in the crystal lattice. The former defect gives rise to no change of density.
Another type of defects are non-stoichometry defects where the cetions and anion are not present in the stoichiometry ratio. In metal excess defect, metal ions or positive ions are in excess as compared to anions of non-metals stoichiometrycally. On the other hand in metal deficiency defect, the cations are in lesser proportion than stoichiometric value. Since the crystal is neutral electrically, the balance of charge is maintained by free electrons or extra positive charges. The metal excess defects gives rise to conduction of electricity due to the presence of free electrons. Also crystals having metal excess defects are paramagnetic and coloured due to the presence of electrons in the anion vacancies.
Impurity defects arise when some foreign atoms are present at the lattice sites in place of the host atoms or at the vacant interstitial sites.
When 15 group elements like P or are doped into Si or Ge, the added impurity atoms occupy the lattice sites forming four covalent bonds with 4 Si/Ge atoms leaving an extra electron free to move. Such a crystal is said to be n-type semi conductor because the conduction of electricity is due to movement of extra unbounded electrons.
If doping of a covalent crystal of 14 group elements are caused by addition of small amounts of elements are caused by addition of small amounts of elements of group 13, e.g, Al or Ga with three valence electrons, one covalent bond formed will be electron deficient and acts as a positive hole. The presence of such holes in the crystal leads to electrical conductivity and the the crystal is said to be p-type semiconductor.
Lattice defect per 1015NaCl is 1. What is the number of lattice defects in 1 mole of NaCl?
View Solution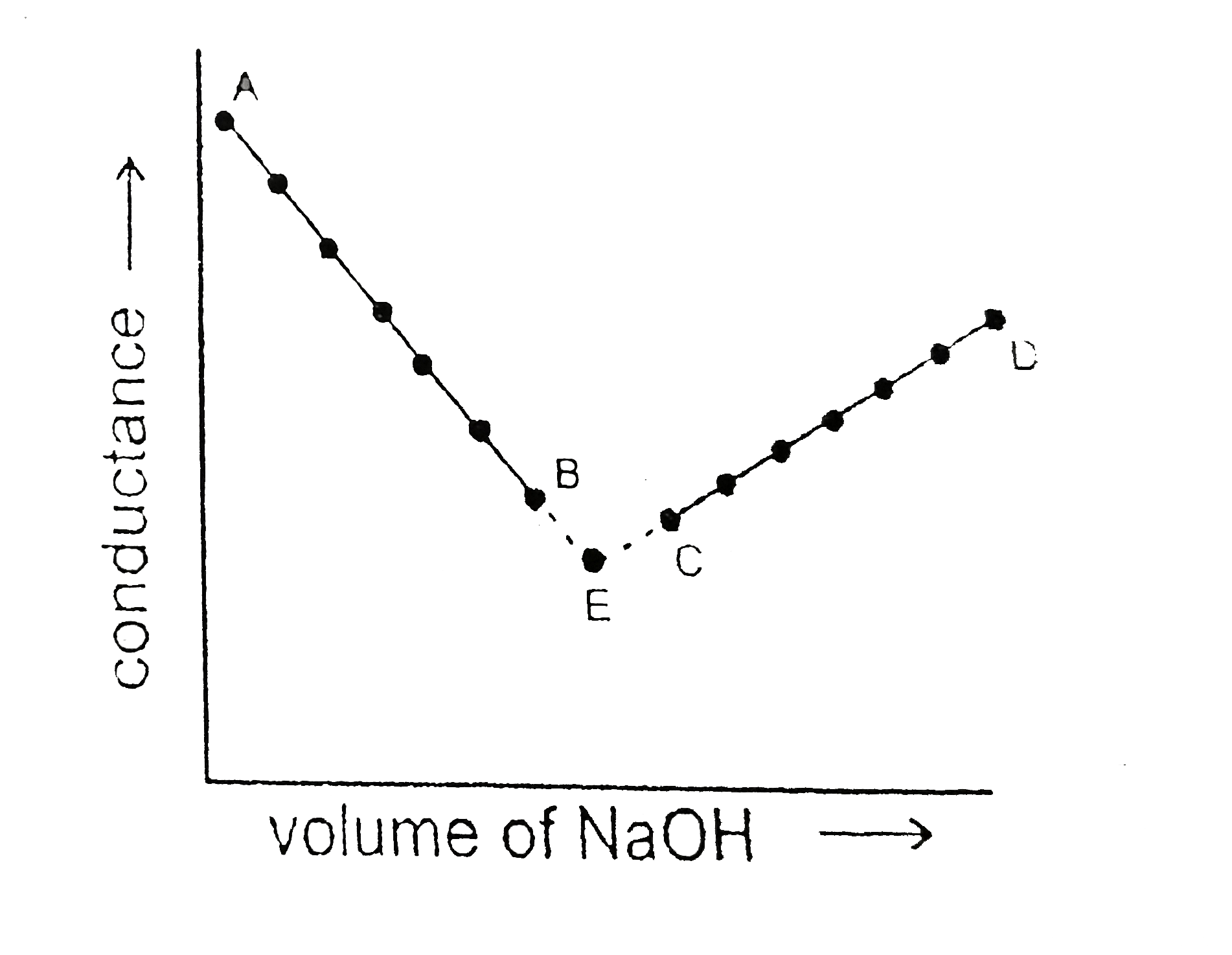
Strong acid versus strong base:
The principle of conductometric titrations is based on the fact that during the titration, one of the ions is replaced by the other and invariable these two ions differ in the ionic conductivity with the result that thhe conductivity of the solution varies during the course of the titration. take, for example, the titration between a strong acid, say HCl, and a string base, say NaOH before NaOH is added, the conductance of HCl solution has a high value due to the presence of highly mobile hydrogen ions. As NaOH is added, H+ ions are replaced by relatively slower moving Na+ ions. consequently the conductance of the solution decreases and this continues right upto the equivalence point where the solution contains only NaCl. Beyond the equivalence point, if more of NaOH is added, then the solution contains a excess of the fast moving OH− ions with the result that its conductance is increased ad it condinues to increase as more and more of NaOH is added. If we plot the conductance value versus the amount of NaOH added, we get a curve of the type shown in Fig. The descending portion AB represents the conductances before the equivalence point (solution contains a mixture of acid HCl and the salt NaCl) and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCl and the excess of NaOH). The point E which represent the minium conductance is due to the solution containing only NaCl with no free acid or alkali and thus represents the equivalence point. this point can, however, be obtained by the extrapolation of the lines AB and DC, and therefore, one is not very particular in locating this point expermentally as it is in the case of ordinary acid-base titrations involving the acid-base indicators.
Weak acid versus strong base:
Let us take specific example of acetic acid being titrated against NaOH. Before the addition of alkali, the solution shows poor conductance due to feeble ionization of acetic acid. Initially the addition of alkali causes not only the replacement of H+ by Na+ but also suppresses the dissociation of acetic acid due to the common ion Ac− and thus the conductance of the solution decreases in the beginning. but very soon the conductance start increasing as addition of NaOH neutralizes the undissociated HAc to Na+Ac− thus causing the replacement of non-conducting HAc with Strong-conducting electrolyte Na+Ac−. the increase in conductance continuous right up to the equivalence point. Beyond this point conductance increases more rapidly with the addition of NaOH due to the highly conducting OH− ions, the graph near the equivalence point is curved due to the hydrolysis of the salt NaAc. The actual equivalence point can, as usual, be obtained by the extrapolation method.
In all these graphs it has been assumed that the volume change due addition of solution from burrette is negnigible, hence volume change of the solution in beaker the conductance of which is measured is almost constant throughout the measurement.
Q. If a 100 mL solution of 0.1 M HBr is titrated using a very concentrated solution of NaOH, then the conductivity (specific conductance) of this solution at the equivalence point will be (assume volume change is negligible due to addition of NaoH) report your answer after multipling it with 10 in Sm−1
[Given λ∘(Na+)=8×10−3Sm2mol−1,λ∘(Br−)=4×10−3Sm2mol−1]
View Solution
Strong acid versus strong base:
The principle of conductometric titrations is based on the fact that during the titration, one of the ions is replaced by the other and invariable these two ions differ in the ionic conductivity with the result that thhe conductivity of the solution varies during the course of the titration. take, for example, the titration between a strong acid, say HCl, and a string base, say NaOH before NaOH is added, the conductance of HCl solution has a high value due to the presence of highly mobile hydrogen ions. As NaOH is added, H+ ions are replaced by relatively slower moving Na+ ions. consequently the conductance of the solution decreases and this continues right upto the equivalence point where the solution contains only NaCl. Beyond the equivalence point, if more of NaOH is added, then the solution contains a excess of the fast moving OH− ions with the result that its conductance is increased ad it condinues to increase as more and more of NaOH is added. If we plot the conductance value versus the amount of NaOH added, we get a curve of the type shown in Fig. The descending portion AB represents the conductances before the equivalence point (solution contains a mixture of acid HCl and the salt NaCl) and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCl and the excess of NaOH). The point E which represent the minium conductance is due to the solution containing only NaCl with no free acid or alkali and thus represents the equivalence point. this point can, however, be obtained by the extrapolation of the lines AB and DC, and therefore, one is not very particular in locating this point expermentally as it is in the case of ordinary acid-base titrations involving the acid-base indicators.
Weak acid versus strong base:
Let us take specific example of acetic acid being titrated against NaOH. Before the addition of alkali, the solution shows poor conductance due to feeble ionization of acetic acid. Initially the addition of alkali causes not only the replacement of H+ by Na+ but also suppresses the dissociation of acetic acid due to the common ion Ac− and thus the conductance of the solution decreases in the beginning. but very soon the conductance start increasing as addition of NaOH neutralizes the undissociated HAc to Na+Ac− thus causing the replacement of non-conducting HAc with Strong-conducting electrolyte Na+Ac−. the increase in conductance continuous right up to the equivalence point. Beyond this point conductance increases more rapidly with the addition of NaOH due to the highly conducting OH− ions, the graph near the equivalence point is curved due to the hydrolysis of the salt NaAc. The actual equivalence point can, as usual, be obtained by the extrapolation method.
In all these graphs it has been assumed that the volume change due addition of solution from burrette is negnigible, hence volume change of the solution in beaker the conductance of which is measured is almost constant throughout the measurement.
Q. The nature of curve obtained for the titration between weak acid versus strong base as described in the above passage will be:
View Solution
Strong acid versus strong base:
The principle of conductometric titrations is based on the fact that during the titration, one of the ions is replaced by the other and invariable these two ions differ in the ionic conductivity with the result that thhe conductivity of the solution varies during the course of the titration. take, for example, the titration between a strong acid, say HCl, and a string base, say NaOH before NaOH is added, the conductance of HCl solution has a high value due to the presence of highly mobile hydrogen ions. As NaOH is added, H+ ions are replaced by relatively slower moving Na+ ions. consequently the conductance of the solution decreases and this continues right upto the equivalence point where the solution contains only NaCl. Beyond the equivalence point, if more of NaOH is added, then the solution contains a excess of the fast moving OH− ions with the result that its conductance is increased ad it condinues to increase as more and more of NaOH is added. If we plot the conductance value versus the amount of NaOH added, we get a curve of the type shown in Fig. The descending portion AB represents the conductances before the equivalence point (solution contains a mixture of acid HCl and the salt NaCl) and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCl and the excess of NaOH). The point E which represent the minium conductance is due to the solution containing only NaCl with no free acid or alkali and thus represents the equivalence point. this point can, however, be obtained by the extrapolation of the lines AB and DC, and therefore, one is not very particular in locating this point expermentally as it is in the case of ordinary acid-base titrations involving the acid-base indicators.
Weak acid versus strong base:
Let us take specific example of acetic acid being titrated against NaOH. Before the addition of alkali, the solution shows poor conductance due to feeble ionization of acetic acid. Initially the addition of alkali causes not only the replacement of H+ by Na+ but also suppresses the dissociation of acetic acid due to the common ion Ac− and thus the conductance of the solution decreases in the beginning. but very soon the conductance start increasing as addition of NaOH neutralizes the undissociated HAc to Na+Ac− thus causing the replacement of non-conducting HAc with Strong-conducting electrolyte Na+Ac−. the increase in conductance continuous right up to the equivalence point. Beyond this point conductance increases more rapidly with the addition of NaOH due to the highly conducting OH− ions, the graph near the equivalence point is curved due to the hydrolysis of the salt NaAc. The actual equivalence point can, as usual, be obtained by the extrapolation method.
In all these graphs it has been assumed that the volume change due addition of solution from burrette is negnigible, hence volume change of the solution in beaker the conductance of which is measured is almost constant throughout the measurement.
Q. The most appropriate titration curve obtained when a mixture of a strong acid (say HCl) and a weak acid (say CH3COOH) is titrated with a strong base (say NaOH) will be
View Solution
