Let $A and B$ be two distinct points on the parabola $y^{2} = 4 x$ . If the axis of the parabola touches a circle of radius $r$ having $A B$ as its diameter, then the slope of the line joining $A and B$ can be (A) $- \frac{1}{r}$ (B) $\frac{1}{r}$ (C) $\frac{2}{r}$ (D) $- \frac{2}{r}$

A

$- \frac{1}{r}$

B

$\frac{1}{r}$

C

$\frac{2}{r}$

D

$- \frac{2}{r}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C, D

Here, coordinate $M = (\frac{t_{1}^{2} + t_{2}^{2}}{2}, t_{1} + t_{2})$ i.e., mid-point of chord AB.

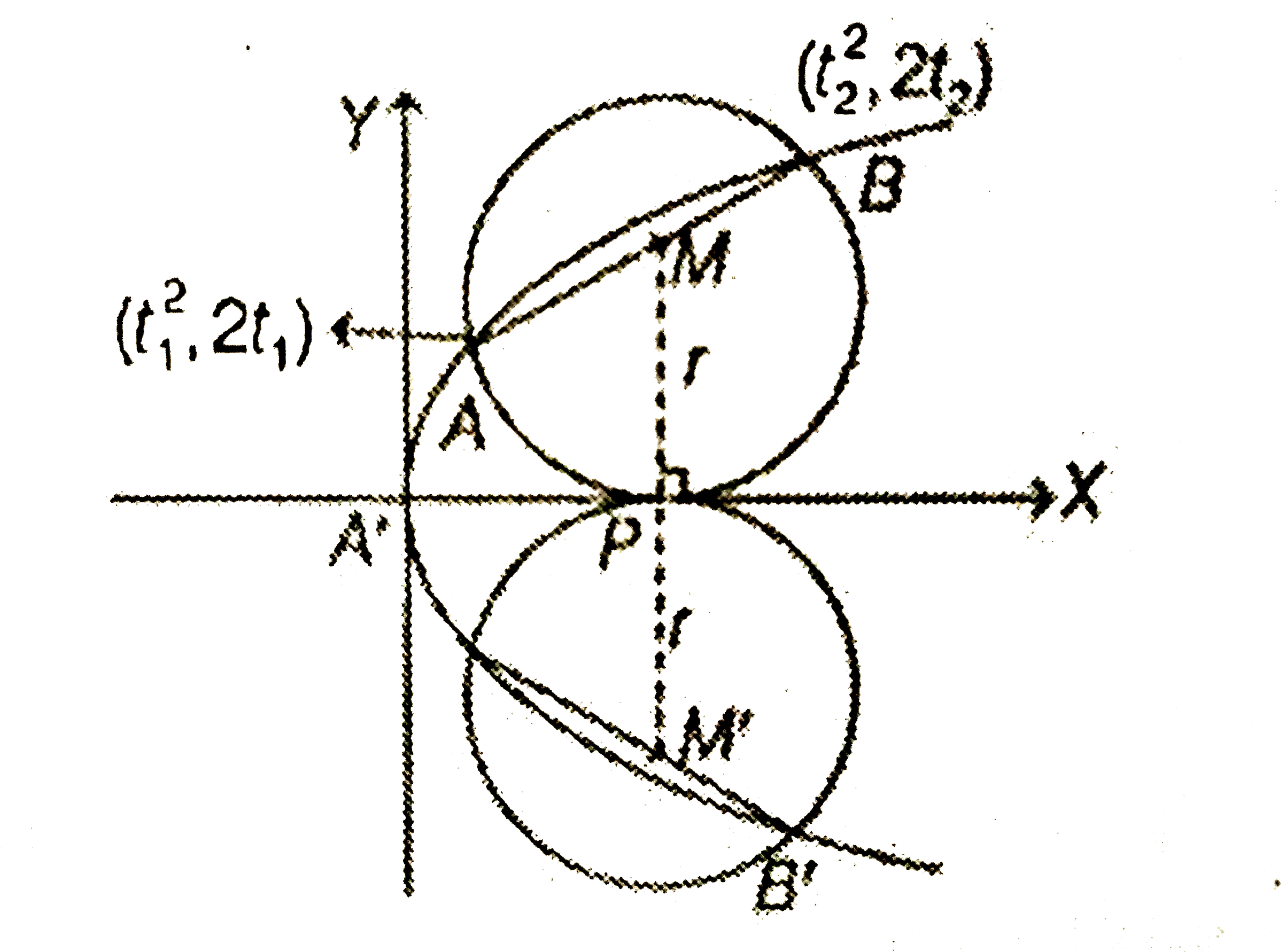
$M P = t_{1} + t_{2} = r$
Also, $m_{A B} = \frac{2 t_{2} - 2 t_{1}}{t_{2}^{2} - t_{1}^{2}} = \frac{2}{t_{2} + t_{1}}$ [when AB is chord]
$\Rightarrow m_{A B} = \frac{2}{r}$ [from Eq. (i)]
Also, $m_{A B} = - \frac{2}{r}$ [when A'B' is chord]
Hence, (c,d) are the correct options.

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let A and B be two distinct points on the parabola $y^{2} = 4 x$ . If the axis of the parabola touches a circle of radius r having AB as its diameter, then the slope of the line joining A and B can be
A $- 1 / r$
B $1 / r$
C $2 / r$
D $- 2 / r$
Question 2 - Select One
Let $A (x_{1}, y_{1}) and B (x_{2}, y_{2})$ be two points on the parabola $y^{2} = 4 a x$ . If the circle with chord AB as a diameter touches the parabola, then $| y_{1} - y_{2} | =$
A4a
B8a
C $6 \sqrt{2} a$
Dnone of these
Question 3 - Select One
Let $A (x_{1}, y_{1})$ and $B (x_{2}, y_{2})$ be two points on the parabola $y^{2} = 4 a x$ . If the circle with chord AB as a dimater touches the parabola, then $| y_{1} - y_{2} |$ is equal to
A $4 a$
B $8 a$
C $6 \sqrt{2} a$
Dnot a constant

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 4 DIAMETER, CHORD OF CONTACT, CHORD BISECTED AND PRODUCT OF PAIR OF TANGENTS OBJECTIVES QUESTION II (ONE OR MORE THAN ONE CORRECT OPTION )

Home
Ask Doubt
Profile