Tangent and normal are drawn at P(16,16) on the parabola y2=16x which intersect the axis of the parabola at A and B respectively. If C is the centre of the circle through the points P,A and B and ∠CPB=θ then the value of tanθ is
12
2
3
43
The correct Answer is:B
Equation of tangent and normal to the curve y2=16x at (16, 16) is x−2y+16=0 and 2x+y−48=0 respectively.
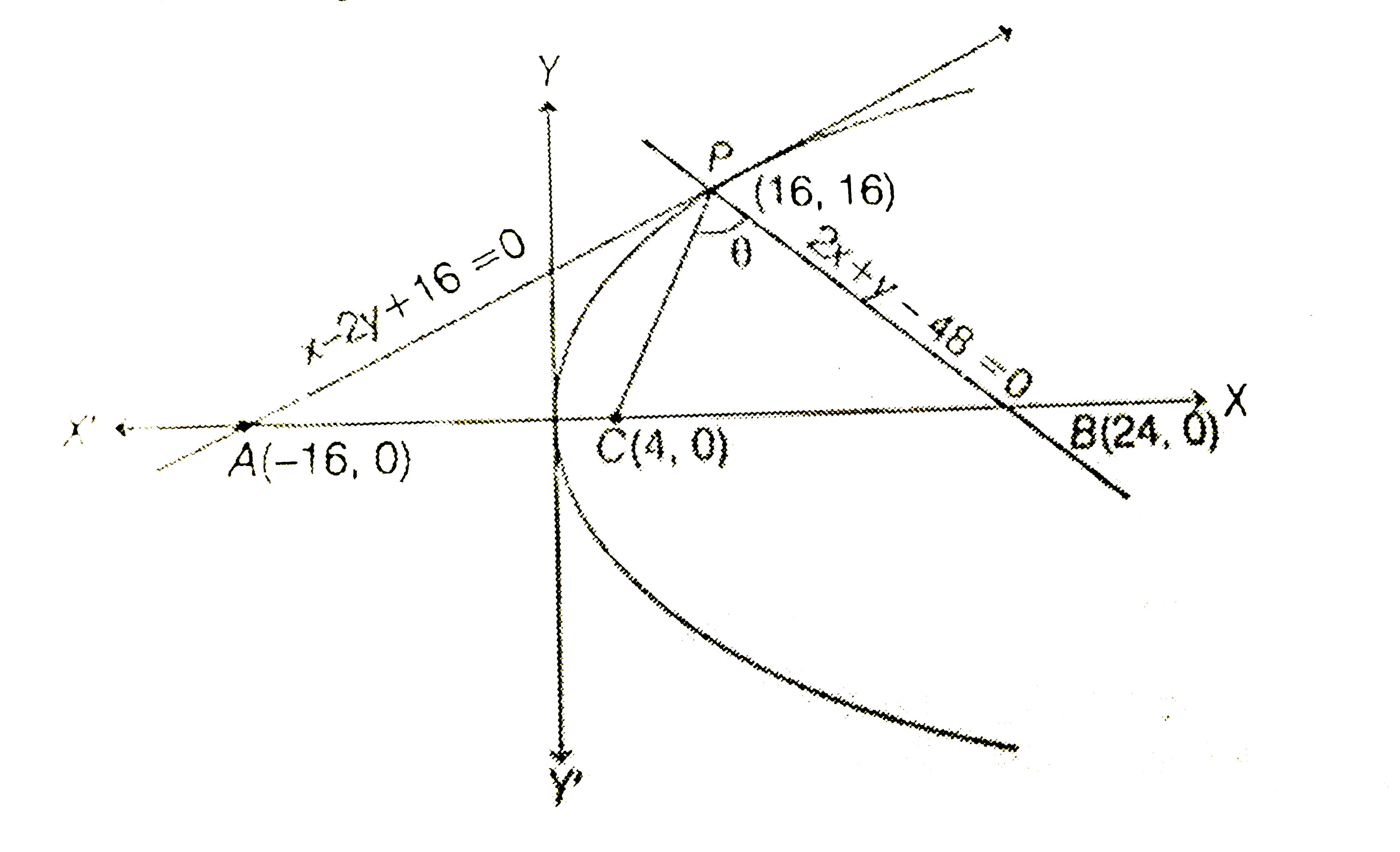
A=(−16,0)B=(24,0)
∵C is the centre of circle passing through PAB i.e.,
Slope of PC=16−016−4=1612=43=m1
Slope of PB=16−016−24=16−8=−m2
tanθ=∣∣∣m1−m21+m1m2∣∣∣
⇒tanθ=∣∣
∣
∣∣43+21−(43)(2)∣∣
∣
∣∣⇒tanθ=2
Topper's Solved these Questions
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 2 EQUATION OF TANGENTS AND PROPERTIES (ASSERTION AND REASON )
Explore 1 Video
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 2 EQUATION OF TANGENTS AND PROPERTIES OBJECTIVES QUESTIONS II (ONE OR MORE THAN CORRECT OPTION )
Explore 1 Video
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (INTERGER )
Explore 2 Videos
- MISCELLANEOUSBook:IIT JEE PREVIOUS YEARChapter:MISCELLANEOUSExercise:MISCELLANEOUS
Explore 87 Videos
- PERMUTATIONS AND COMBINATIONSBook:IIT JEE PREVIOUS YEARChapter:PERMUTATIONS AND COMBINATIONSExercise:Dearrangement and Number of Divisors (Fill in the Blank )
Explore 1 Video
Similar Questions
Tangent and normal are drawn at the point P≡(16,16) of the parabola y2=16x which cut the axis of the parabola at the points AandB , rerspectively. If the center of the circle through P,A,andB is C , then the angle between PC and the axis of x is (a)tan−1(12) (b) tan−12 (c)tan−1(34) (d) tan−1(43)
View SolutionA tangent and a normal are drawn at the point P(8, 8) on the parabola y2=8x which cuts the axis of the parabola at the points A and B respectively. If the centre of the circle through P, A and B is C, then the sum f sin(∠PCB) and cot(∠PCB) is equal to
View Solution
Knowledge Check
A tangent and a normal are drawn at the point P (16,16) of the parabola y2=16x which cut the axis of the parabola at the points A and B respectively. If the centre of the through P, A and B is C, then angle between PC and axis of x is :
Atan−112Btan−12Ctan−134Dtan−143Find the axis of the parabola x2=16y.
Ax=0By=0Cx=4Dx+y=0The tangent and normal at the point p(18, 12) of the parabola y2=8x intersects the x-axis at the point A and B respectively. The equation of the circle through P, A and B is given by
Ax2+y2+4x−540=0Bx2+y2−6x−360=0Cx2+y2−4x−396=0Dx2+y2−2x−444=0
For the parabola y2=8x tangent and normal are drawn at P(2.4) which meet the axis of the parabola in A and B .Then the length of the diameter of the circle through A,P,B is
View SolutionA tangent and a normal are drawn at the point P(2,-4) on the parabola y2=8x, which meet the directrix of the parabola at the points A and B respectively. If Q (a,b) is a point such that AQBP is a square , then 2a+b is equal to :
View SolutionNormals are drawn at points P, Q are R lying on the parabola y2=4x which intersect at (3, 0), then

View SolutionNormals are drawn at points A,B,andC on the parabola y2=4x which intersect at P. The locus of the point P if the slope of the line joining the feet of two of them is 2, is
View SolutionThe tangent and normal at the point P(4,4) to the parabola, y2=4x intersect the x-axis at the points Q and R, respectively. Then the circumcentre of the ΔPQR is
View Solution

