The axis of parabola is along the line y=x and the distance of its vertex and focus from origin are √2 and 2√2 respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is :
The correct Answer is:A
Since, distance of vertex from origin is √2 and focus is 2√2
∴ V (1,1) and f (2,2) (i.e. lying on y = x)
where, length of latusretum
=4a=4√2
∴ By definition of parabola
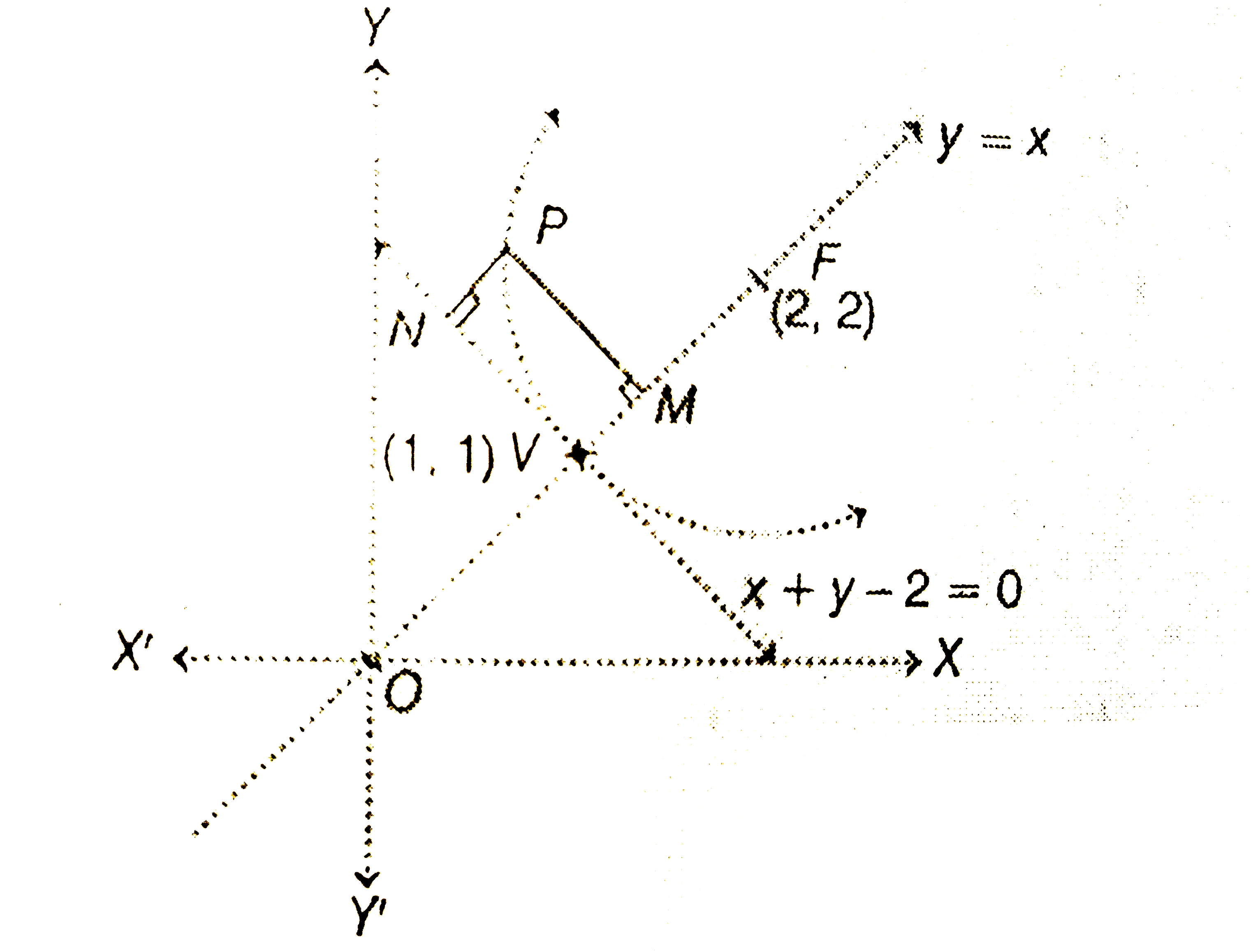
PM2=(4a)PN)
Where, PN is length of perpendicular upon
x+y−2=0, i.e., tangent at vertex
⇒(x−y)22=4√2(x+y−2√2)
⇒(x−y)2=8(x+y−2)
Topper's Solved these Questions
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (ASSERTION AND REASON )
1 Videos
- PARABOLABOOK - IIT JEE PREVIOUS YEARCHAPTER - PARABOLAEXERCISE - TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (INTERGER )
2 Videos
- MISCELLANEOUSBOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS
87 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Dearrangement and Number of Divisors (Fill in the Blank )
1 Videos
Similar Questions
The axis of parabola is along the line y=x and the distance of its vertex and focus from origin are √2 and 2√2 respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is :
View SolutionThe axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (x+y)2=(x−y−2) (x−y)2=(x+y−2) (x−y)2=4(x+y−2) (x−y)2=8(x+y−2)
View Solution
Knowledge Check
The axis of a parabola is along the line y = x and the distance of its vertex from origin is √2 and that from its focus is 2√2. If vertex and focus both lie in the first quadrant, then the equation of the parabola is
A(x+y)2=(x−y−2)B(x−y)2=(x+y−2)C(x−y)2=4(x+y−2)D(x−y)2=8(x+y−2)If (0,4) and (0,2) are respectively the vertex and focus of a parabola, then its equation is
Ax2+8y=16Bx2+8y=32Cx2+16y=30Dx2−8y=32The axis of a parabola is along the line y = x and its vertex and focus are in the first quadrant at distances √2,2√2 respectively, from the origin. The equation of the parabola, is
A(x+y)2=x−y−2B(x−y)2=x−y−2C(x−y)2=(x−y−2)D(x−y)2=8(x+y−2)
If the points (0,4)and(0,2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
View SolutionA parabola has its vertex and focus in the first quadrant and axis along the line y=x . If the distances of the vertex and focus from the origin are respectively √2&2√2 , then equation of the parabola is x2+y2−8x+8y+2xy=16 x2+y2−8x−8y+16=2xy (x−y)2=8(x+y−2) (x+y)2=(x−y+2)
View SolutionIf (0, 3) and (0, 2) are respectively the vertex and focus of a parabola, then its equation, is
View SolutionIf (0,4) and (0,2) are respectively the vertex and focus of a parabola, then its equation is
View SolutionAxis of a parabola is y = x and vertex and focus are at a distance √2 and 2√2 respectively from the origin. Then equation of the parabola is
View Solution
