There si a parabola having axis as x-axis, vertex is at a distance of 2 unit from origin & focus is at (4,0). Which of the following point does not lie on the parabola. (a) (6,8) (b) (5,2√6) (c) (8,4√3) (d) (4,−4)
The correct Answer is:C
According to given information, we have the following figure.
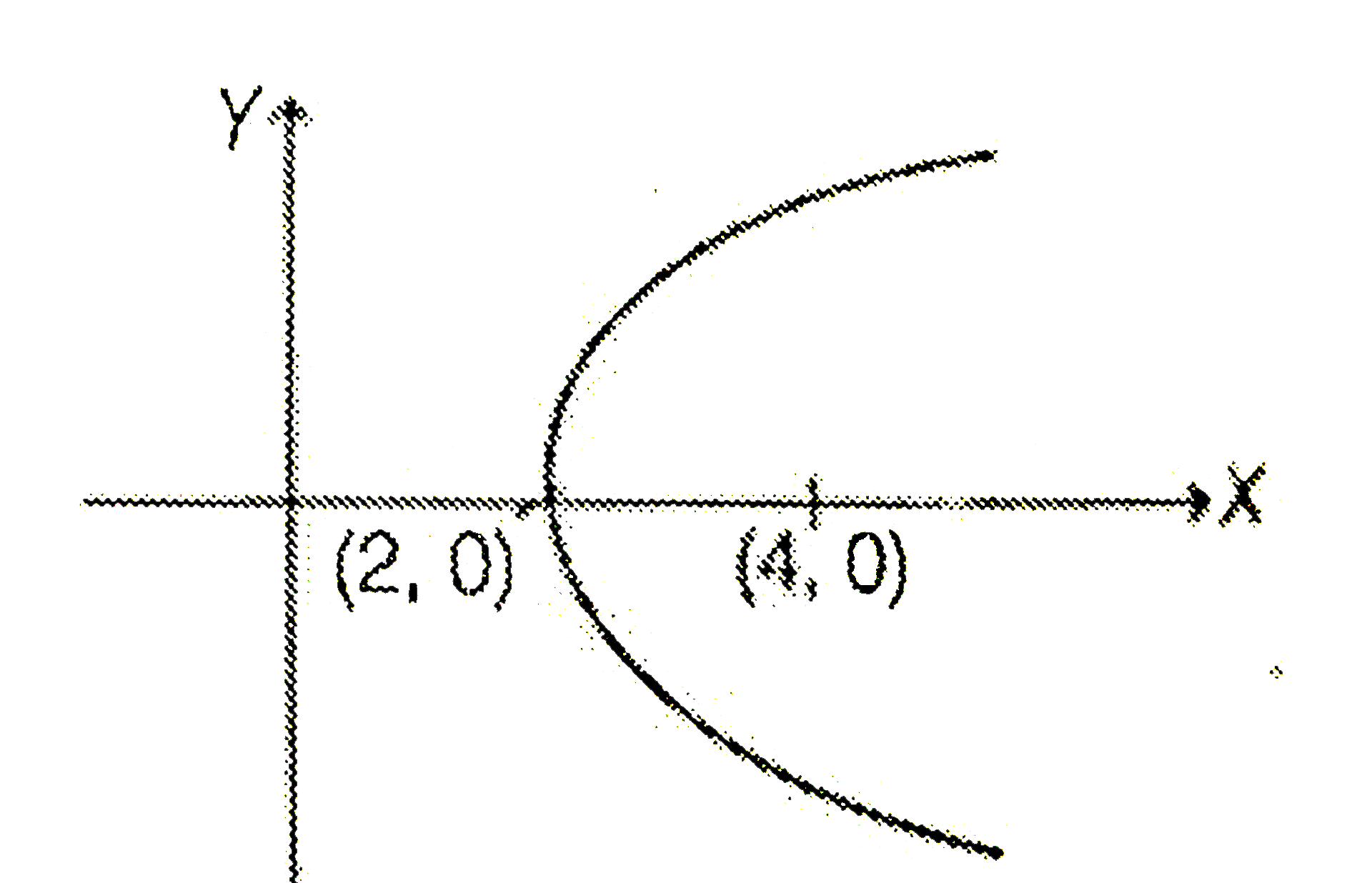
Now, if the origin is shifted to (2,0) and (X,Y) are the coordinates with respect to new origin, then equation of parabola is Y2=4aX,
where, X=x−2 and Y=y and a=4−2=2
∴y2=8(x−2)
Note that (8,6) is the only point which does not satisfy the equation.
Topper's Solved these Questions
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (ASSERTION AND REASON )
Explore 1 Video
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 1 EQUATION OF PARABOLA AND FOCAL CHORD (INTERGER )
Explore 2 Videos
- MISCELLANEOUSBook:IIT JEE PREVIOUS YEARChapter:MISCELLANEOUSExercise:MISCELLANEOUS
Explore 87 Videos
- PERMUTATIONS AND COMBINATIONSBook:IIT JEE PREVIOUS YEARChapter:PERMUTATIONS AND COMBINATIONSExercise:Dearrangement and Number of Divisors (Fill in the Blank )
Explore 1 Video
Similar Questions
If the vertices of the hyperbola be at (−2,0) and (2,0) and one of the foci be at (−3,0) then which one of the following points does not lie on the hyperbola? (a) (−6,2√10) (b) (2√6,5) (c) (4,√15) (d) (6,5√2)
View SolutionThe line x−y+2=0 touches the parabola y2=8x at the point (A) (2,−4) (B) (1,2√2) (C) (4,−4√2 (D) (2,4)
View Solution
Knowledge Check
Axis of a parabola lies along x-axis. If its vertex and focus are at distances 2 and 4, respectively, from the origin on the positive x-axis, then which of the following points does not lie on it ?
A(4, -4)B(5,2√6)C(8, 6)D(6,4√2)If axis of the parabola lie along y-axis and if vertex is at a distance of 2 from origin on positive y-axis, focus is at a distance of 2 from origin on negative y-axis then which of the following points doesn't lie on the parabola:
A(4√2,0)B(4,1)C(−4,−2)D(8,−2)Equation of the parabola whose axis is y=x distance from origin to vertex is √2 and distance from origin to focus is 2√2, is (Focus and vertex lie in Ist quadrant):
A(x+y)2=2(x+y−2)B(x−y)2=8(x+y−2)C(x−y)2=4(x+y−2)D(x+y)2=4(x+y−2)
the length of intercept made by the line √2x−y−4√2=0 on the parabola y2=4x is equal to (a) 6√3 (b) 4√3 (c) 8√2 (d) 6√2
View SolutionLet the length of latus rectum of an ellipse with its major axis along x-axis and center at the origin, be 8. If the distance between the foci of this ellipse is equal to the length of the minor axis , then which of the following points lies on it: (a) (4√2,2√2) (b) (4√3,2√2) (c) (4√3,2√3) (d) (4√2,2√3)
View SolutionThe centre of an ellipse is at origin and its major axis coincides with x-axis. The length of minor axis is equal to distance between foci and passes through the point (√29,2√295), then which of the following points lie on ellipse (A) (4√3,2√2) (B) (4√3,2√3) (C) (4√2,2√3) (D) (4√2,2√2)
View SolutionAxis of a parabola is y = x and vertex and focus are at a distance √2 and 2√2 respectively from the origin. Then equation of the parabola is
View SolutionThe equation of parabola whose vertex and focus lie on the axis of x at distances a and a1 from the origin respectively, is
View Solution