The equation of tangents drawn from the origin to the circlex2+y2−2rx−2hy+h2=0
A
x = 0
B
y = 0
C
(h2−r2)x−2rhy=0
D
(h2−r2)x+2rhy=0
Video Solution
Text Solution
Since, tangents are drawn from origin. So, the equation of tangent be y = mx
⇒ Length of perpendicular from origin = radius
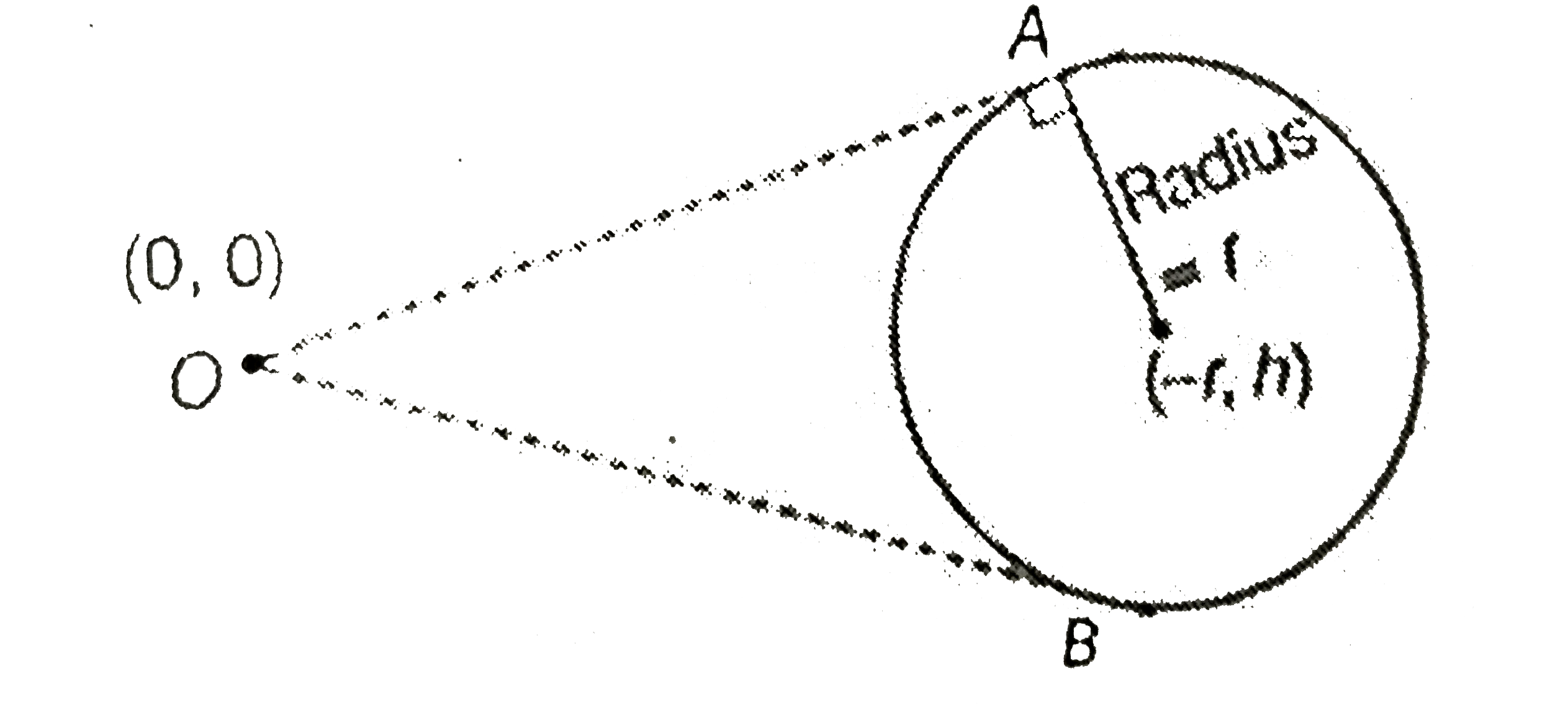
⇒|mr+h|√m2+1=r
⇒m2r2+h2+2mrh=r2(m2+1)
⇒m=∣∣∣r2−h22rh∣∣∣,m=∞
∴ Equation oftangents are y=∣∣∣r2−h22rh∣∣∣x,x=0 Therefore (a) and (c) are the correct answers.
|
Topper's Solved these Questions
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 5 Assertion and Reason
Explore 1 Video
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 5 Fill in the blanks
Explore 7 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 5 (objective Questions I)
Explore 6 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
Explore 1 Video
Similar Questions
Knowledge Check
The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2rhy=0The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2hy=0The equation of tangent drawn from origin to the circle x2+y2−2ax−2by+b2=0 are perpendicular if
Aa2=b2Ba2+b2=1C2a=bD2b=a
A pair of tangents are drawn from the origin to the circle x2+y2+20(x+y)+20=0, The equation of pair of tangent is
View SolutionA pair of tangents are drawn from the origin to the circle x2+y2+20(x+y)+20=0 . Then find its equations.
View SolutionThe equations of the tangents drawn from the origin to the circle x2+y2+2rx+2hy+h2=0, are :
View SolutionThe equation of tangents drawn from the point (0,1) to the circle x2+y2−4x−2y+4=0 are
View SolutionThe tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are perpendicular if
View Solution

