Question

If two distinct chords, drawn from the point (p, q) on the circle $x^2+y^2=px+qy$
(where $pq\ne q)$
are bisected by the x-axis, then
$p^2=q^2$
(b) $p^2=8q^2$

$p^2<8q^2$
(d) $p^2>8q^2$

Options

A. `P^(2)=q^(2)`0
B. P^(2)=8q^(2)`
C. P^(2)lt8q^(2)`
D. `P^(2)gt8q^(2)`

Answer

D

Explanation

NOTE In soving a line and a circle there oftengenerate a quadratic equation and further we have to apply condition of Discrominant so equation convert from coordinate to quadratic equation.
From equation of circle it is clear that circle passes through origin. Let AB is chord of the circle.

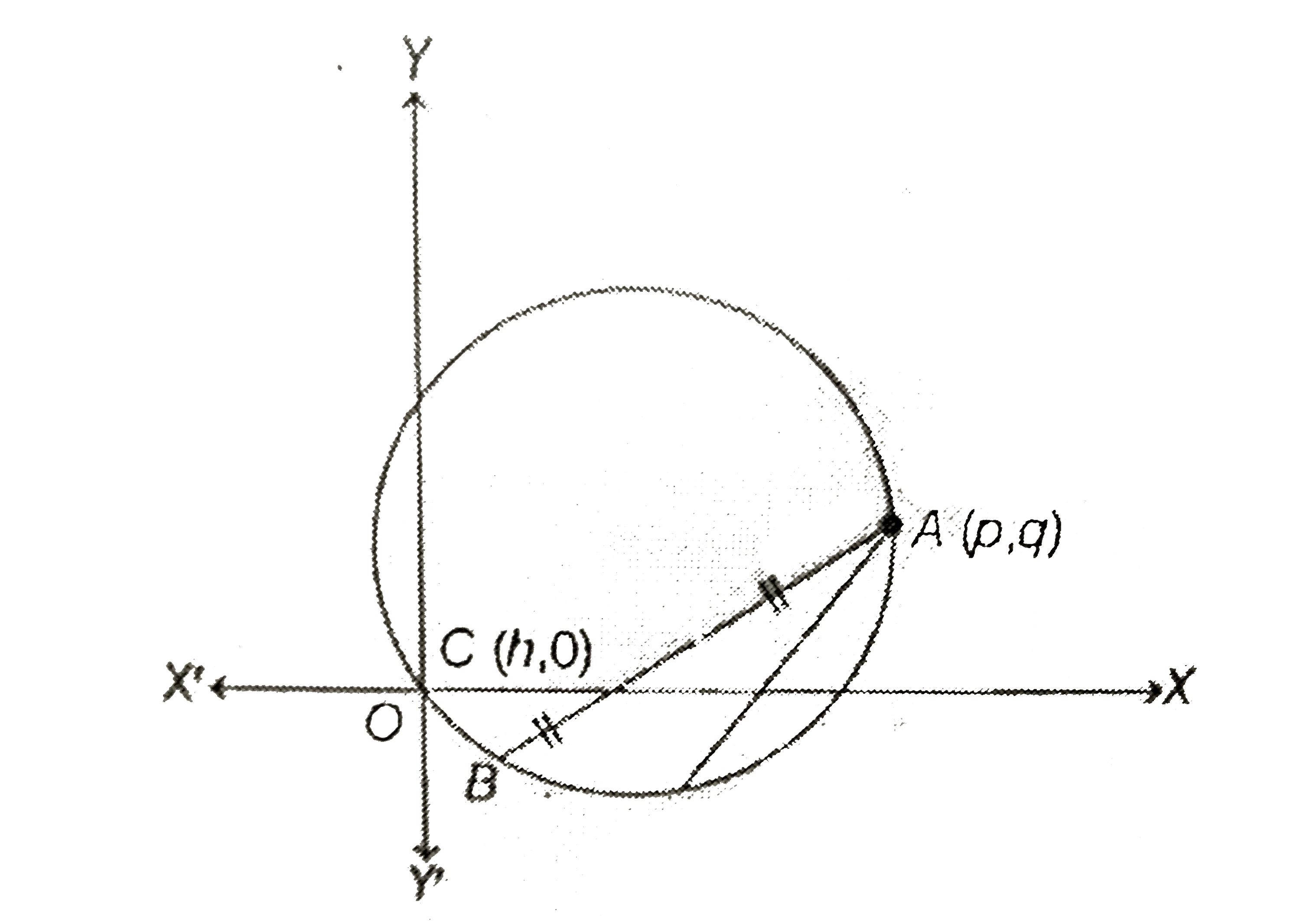
`A -=(p, q) *C` is mid-point and coordinate of C is (h, 0)
Then, coordinates of B are `(-p + 2h)^(2) + (-q)^(2) + P(-P + 2h) + q(-q)`
`rArr p^(2)+4h^(2)-4ph+q^(2)=-p^(2)+2ph-q^(2)`
`rArr 2p^(2)+2q^(2)-6ph+4h^(2)=0`
`rArr 2h^(2)-3ph+p^(2)+q^(2)=0" " ...(i)`
There ar given two distinct chords which are bisected at X- axis then, there will be two distinct value of h satisfying Eq. (i).
So, discriminant of this quardratic equation must be `gt 0`.
`rArr Dgt0`
`rArr (-3p)^(2)-4*2(p^(2)+q^(2))gt0`
`rArr 9p^(2)-8p^(2)-8q^(2)gt0`
`rArr p^(2)-8q^(2)gt0rArr p^(2)gt8q^(2)`