Question

Let $S$
be the circle in the $xy$
-plane defined by the equation $x^2+y^2=4.$
(For Ques. No 15 and 16)
Let $P$
be a point on the circle $S$
with both coordinates being positive. Let the tangent
to $S$
at $P$
intersect the coordinate axes at the points $M$
and $N$
. Then, the mid-point of the line segment $MN$
must lie on the curve

Options

A. `(x-4)^(2)=3xy`
B. `x^(23)+y^(23)=2^(4//3)`
C. `x^(2)+y^(2)=2xy`
D. `x^(2)+y^(2)=x^(2)y^(2)`

Answer

D

Explanation

We have
`x^(2)+y^(2)=4`
Let `P(2 cos theta, 2sintheta)` be a point on a circle.
`therefore` Tangent at P is
` 2costhetax+2sinthetay=4`
`rArr x costheta+ysintheta=2`

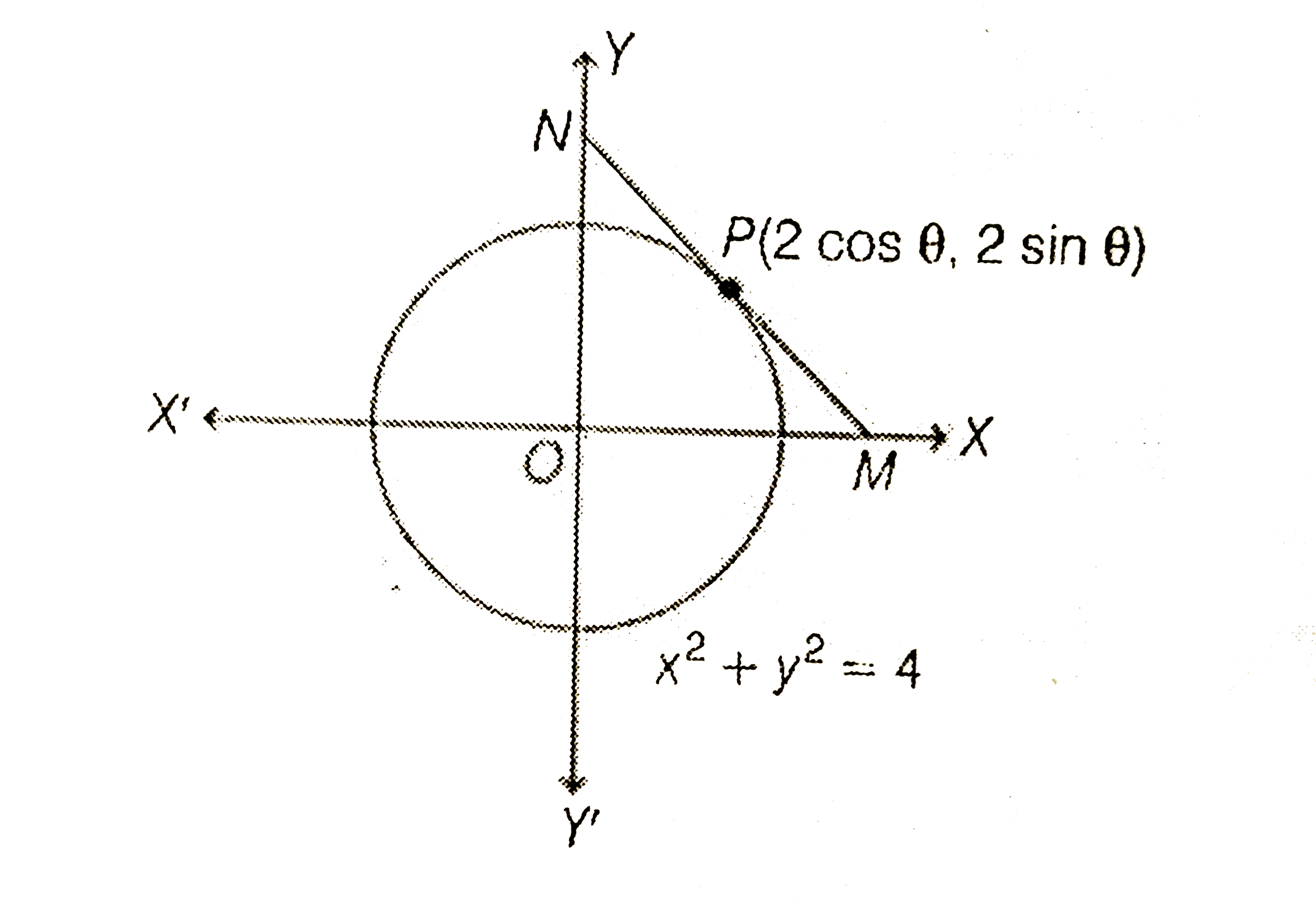
`therefore` The coordinates at `M((2)/(costheta),0)) and N((0,(2)/(sintheta))`
Let (h,k) is mid point of MN
`thereforeh=(1)/(costheta)and k=(1)/(sintheta)`
`rArrcostheta=(1)/(h)and sintheta=(1)/(k)`
`rArrcos^(2)theta+sin^(2)theta=(1)/(h^(2))+(1)/(k^(2))rArr1= (h^(2)+k^(2))/(h^(2)+k^(2))`
`rArrh^(2)+k^(2)=h^(2)k^(2)`
`therefore" Mid-point of MN lie on the curve " x^(2)+y^(2)=x^(2)y^(2)`