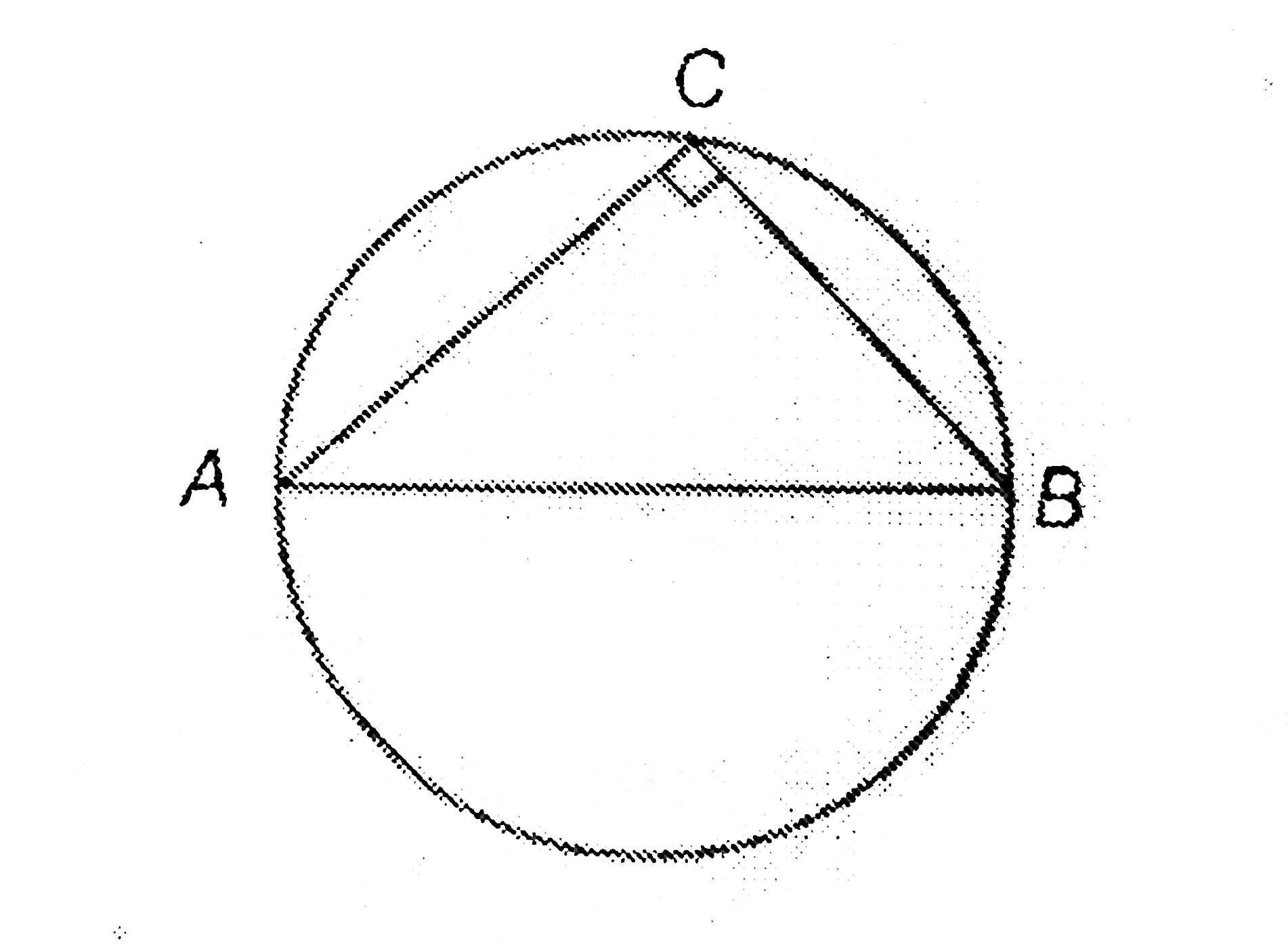
AB is a diameter of a circle and C is any point on the circle. Show that the area of ABC is maximum, when it is isosceles.
the area of ΔABC is maximum when it is isosceles
the area of ΔABC is minimum whne it is isosceles
the perimeter of ΔABC is minimum when it is isosceles
None of the above
The correct Answer is:A
Clearly, ∠C=90∘ as angle in semi-circle is right angled. Now, area of triangle is maximum when AC=BC.
i.e., Triangle is right angled isosceles.
Topper's Solved these Questions
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 1(Objective Question II)
Explore 2 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 1Fill in the blanks
Explore 2 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
Explore 1 Video
Similar Questions
AB is a diameter of a circle and C is any point on the circle. Show that the area of ABC is maximum, when it is isosceles.
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then (a) the area of ΔABC is maximum when it is isosceles (b) the area of ΔABC is minimum when it is isosceles (c) the perimeter of ΔABC is minimum when it is isosceles (d) none of these
View Solution
Knowledge Check
If diameter of a circle is r cm, then the area of a circle is :
Aπr2cm2Bπr24cm2Cπr22cm2D2πrcm2If diameter of a circle is 2r cm, then area of the circle is :
Aπr2cm2B4πr2cm2Cπr22cm2D2πrcm2If diameter of a circle is r2cm, Then the area of a circle is :
Aπr2cm2Bπr216cm2Cπr24cm2Dπrcm2
AB is a diameter of a circle and C is any point on the circumference of the circle. Then
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIf A(3,−4),B(7,2) are the ends of a diameter of a circle and C is a point on the circle then the circumcentre of ABC is
View SolutionIf A(3,-4), B(7,2) are the ends of a diameter of a circle and C(3,2) is a point on the circle then the orthocentre of the ΔABC is
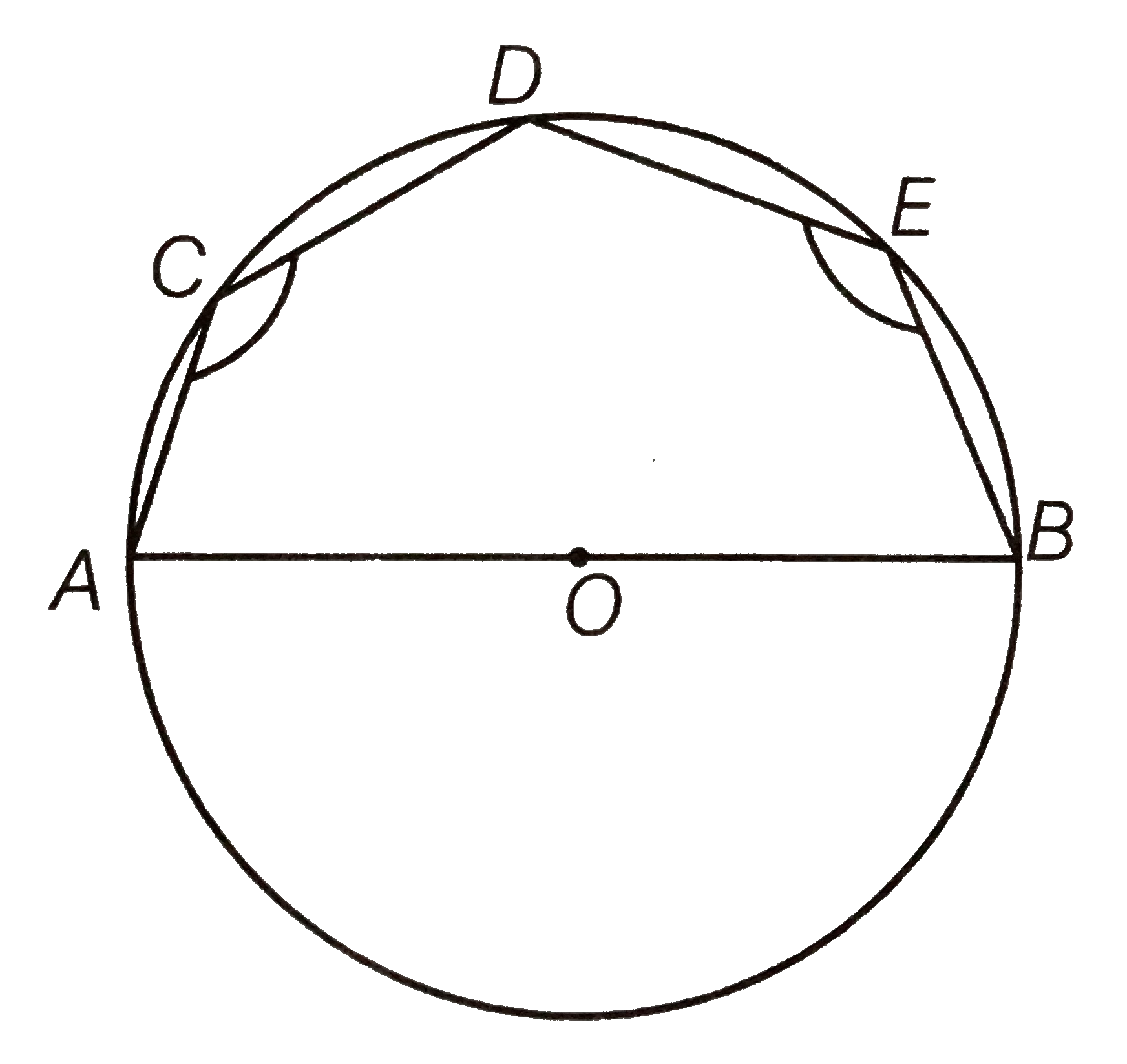
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
View Solution