The centre of circle inscribed in a square formed by lines $x^{2} - 8 x + 12 = 0$ and $y^{2} - 14 y + 45 = 0$ is

A

(4, 7)

B

(7, 4)

C

(9, 4)

D

(4, 9)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Given circle is inscribed in square formed by the lines
$x^{2} - 8 x + 12 = 0 and y^{2} - 14 y + 45 = 0$
$\Rightarrow x = 6 and x = 2, y = 5 and y = 9$
which could be plotted as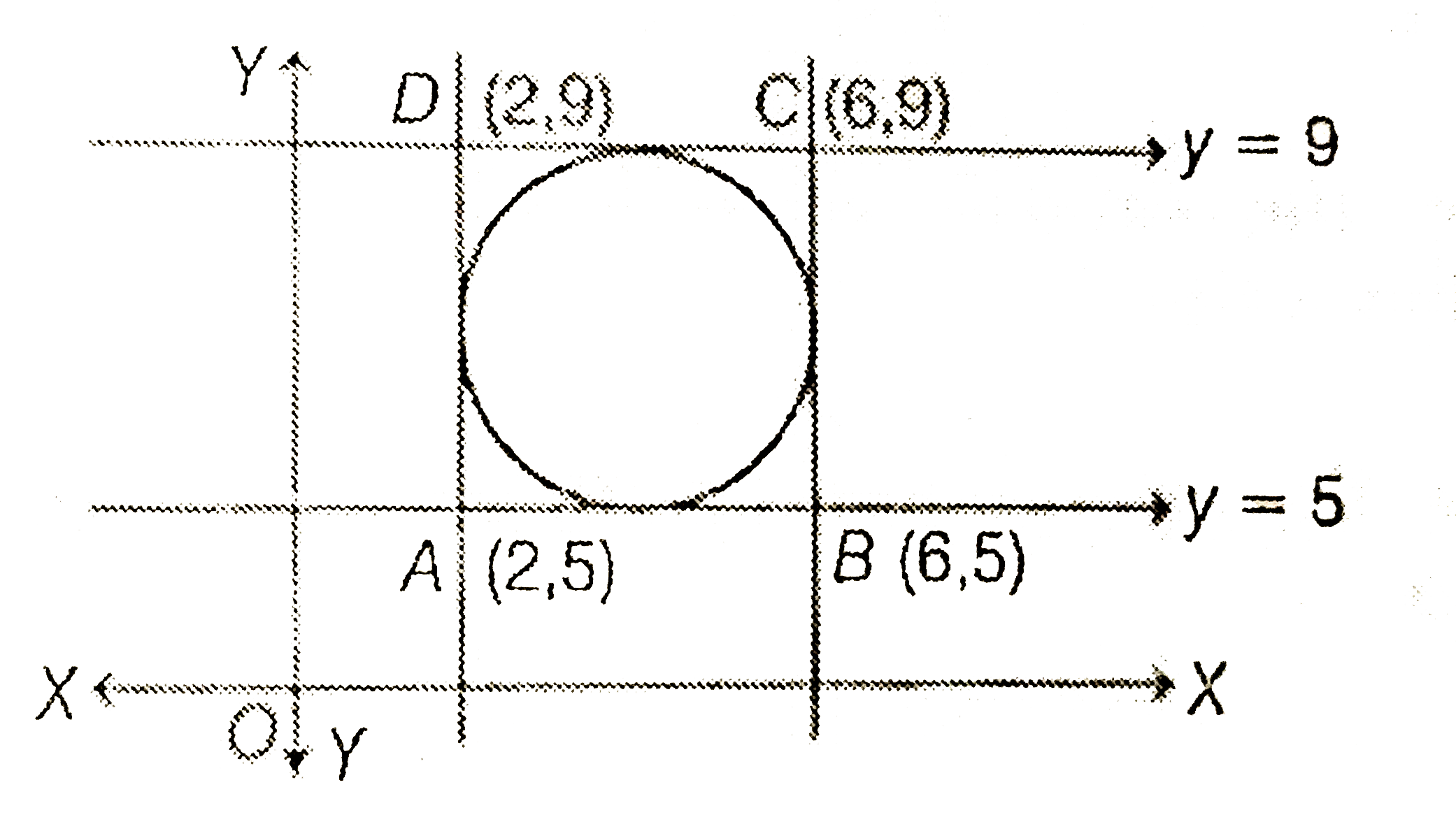
Where, ABCD clearly forms a square.
$∴$ Centre of inscribed circle
= Point of intersection of diagonals
= Mid point of AC or BD
$= (\frac{2 + 6}{2}), (\frac{5 + 9}{2}) = (4, 7)$
$\Rightarrow$ Centre of inscribed circle is (4, 7).

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The centre of circle inscribed in a square formed by lines $x^{2} - 8 x + 12 = 0 a n {d y}^{2} - 14 y + 45 = 0$ is $(4, 7)$ $(7, 4)$ $(9, 4)$ $(4, 9)$
A(4, 7)
B(7, 4)
C(9, 4)
D(4, 9)
The equation of the circumcricle of the $x^{2} - 8 x + 12 = 0 and y^{2} - 14 y + 45 = 0$ is
A $x^{2} + y^{2} - 4 x - 7 y + 57 = 0$
B $x^{2} + y^{2} - 8 x - 14 y + 57 = 0$
C $x^{2} + y^{2} - 8 x - | 14 y + 5 | = 0$
D $2 x^{2} + y^{2} - 8 x - 14 y + 57 = 0$

IIT JEE PREVIOUS YEAR-CIRCLE-Topic 5 Integer Answer type Question

Home
Ask Doubt
Profile