Let w = (√3+ι2) and P={wn:n=1,2,3,.....}, Further H1={z∈C:Re(z)>12}andH2={z∈c:Re(z)<−12} Where C is set of all complex numbers. If z1∈P∩H1,z2∈P∩H2 and O represent the origin, then ∠Z1OZ2 =
A
π2
B
π6
C
2π3
D
(5π6)
Video Solution
Text Solution
The correct Answer is:C, D
PLAN It is the simple representaion of points on Argand plane and to find the angle between the points.
Here, P=Wn=(cosπ6+Isinπ6)n=cosnπ6+isin(nπ6)
H={z∈C:Re(z)>12}
∴P∩H1 represents those points for which cod nπ6 is + ve .
Hence , it belongs to I or IV quradrant .
⇒z1=P∩H1=cosπ6+isinπ6cos11π6+isin11π6
∴z1=√32+i2or√32−i2
Similarly z2=P∩H2 i.e those points for which
cos nπ6<0
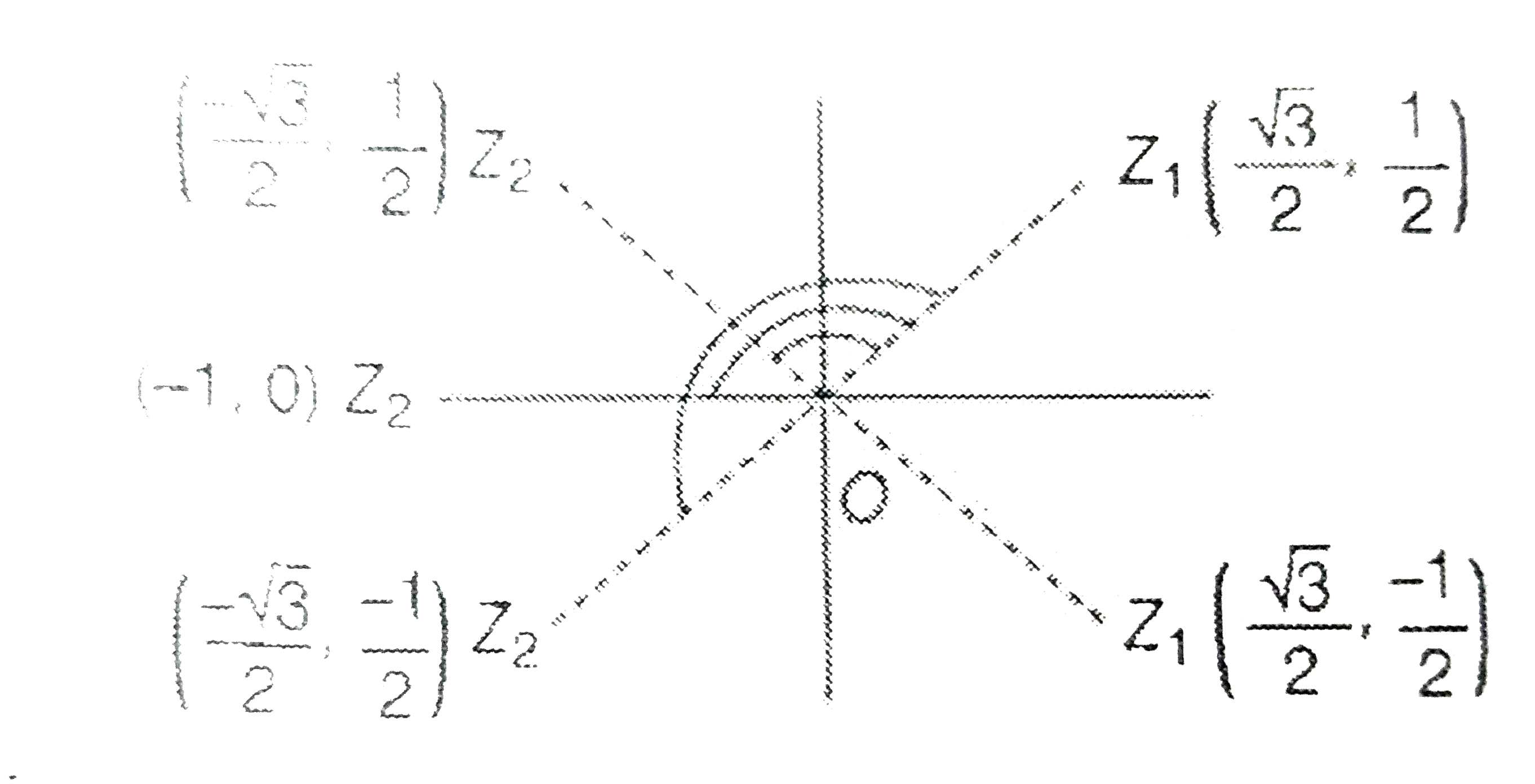
∴z2=cosπ+isinπ,cos(5π)6+isin(5π)6,cos7π6+isin(7π)6
⇒z1=−1,−√32+i2,−√32−i2
Thus ∠z1Oz2=2π3,5π6,π
|
Topper's Solved these Questions
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 4 ROTATION OF A COMPLEX NUMBER (FILL IN THE BLANKS )
Explore 3 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 4 ROTATION OF A COMPLEX NUMBER (ANALYTICAL & DESCRIPTIVE QUESTIONS)
Explore 7 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 4 ROTATION OF A COMPLEX NUMBER (OBJECTIVE QUESTION I)(ONLY ONE CORRECT OPTION)
Explore 6 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 5 Integer Answer type Question
Explore 1 Video
- DEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:DEFINITE INTEGRATIONExercise:LIMITS AS THE SUM
Explore 6 Videos
Similar Questions
Knowledge Check
Let ω=√3+i2 and P={Wn:n1,2,3………} further
H1={z∈C:Re(z)>12}
and H2={z∈C:Re(z)<−12}, where C is the set of all complex numbers. If z∈P∩H2 and 0 represents the origin then ∠z10z2=Aπ2Bπ6C2π3D5π6If z1,z2,z3 are in H.P., they lie on a
AcircleBsphereCstraight lineDnone of theseLet C be the set of all complex numbers. Let Si={z in C||z-3-2i|^(2)=8}, S2= {z∈C∣|z−¯z|≥8} and S3= {z∈C∣Re(z)≥5}. Then the number of elements in S1∩S2∩S3 is equal to
A1B0C2DInfinite
For all complex number z1,z2 satisfying |z1|=12 and |z2−3−4ι|=5,then |z2−ιz1|
View SolutionIf the points represented by complex numbers z1=a+ib,z2=c+z1−z2 are collinear, where i=√−1, then
View SolutionIf z1=a+ib and z2=c+ are two complex numbers then z1>z2 is meaningful if
View SolutionThe set {Re(2iz1−z2):zisacomplexνmber,|z|=1,z=±1} is________.
View SolutionLet |z|=2andw−z+1z−1,wherez,w,∈C (where C is the set of complex numbers). Then product of least and greatest value of modulus of w is__________.
View Solution