Let Z 1 and Z 2 , be two distinct complex numbers and let w = ( 1 - t ) z 1 + t z 2 for some number "t" with o

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:a,c,d

Given z = ( 1 - t ) z 1 + j t z 2 ( 1 - t ) + t
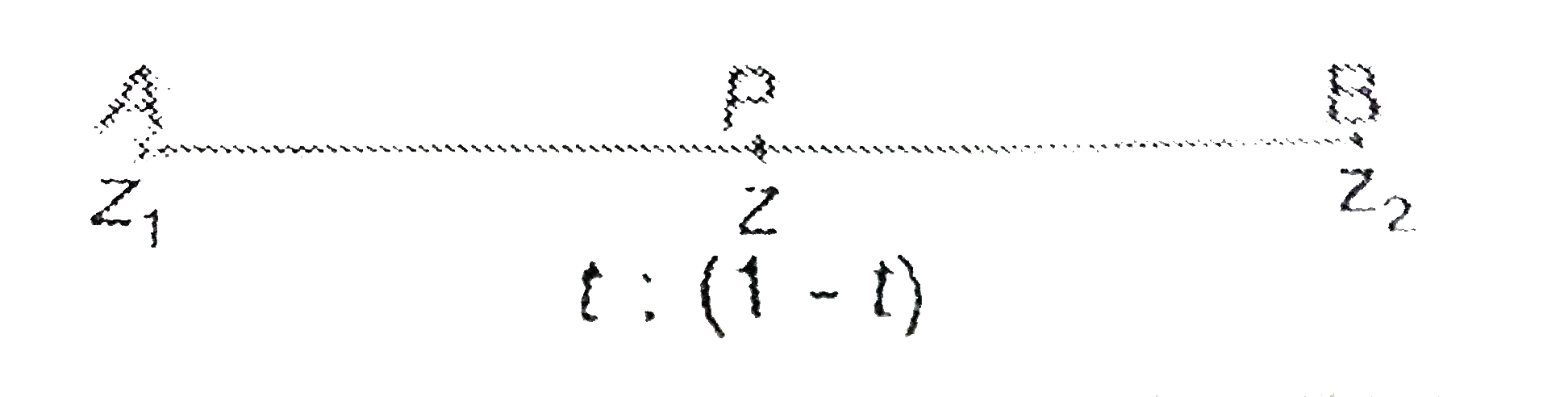
ocr_image
Clearly z divides z 1 and z 2 in the ratio of t : ( 1 - t ) , 0 < t < 1
⇒ A P + B P = A B i e | z - z 1 | + | z + z 2 | = | z 1 - z 2 |
⇒ option (a) is true
Also a r g ( z - z 1 ) = a r g ( z 2 - z 1 )
⇒ a r g ( ( z - z 1 ) ( z 2 - z 1 ) ) = 0
∴ z z _ 1 z 2 - z 1 is purely real .
⇒ z - z 1 z 2 - z 1 = z ¯ - z 1 z 2 - z ¯ 1
or | z - z 1 z ¯ - z ¯ 1 z 2 - z 1 z ¯ 2 - z ¯ 1 | = 0
Option (c ) is correct

Updated on:21/07/2023
|
Class 12MATHSCOMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+iz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then

    A|z−z1|+|z−z2 =|z1−z2∣
    Barg(z−z1)=arg(z−z2)
    C∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0
    Darg(z−z1)=arg(z2−z1)

  • Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+iz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then

    A|z−z1|+|z−z2|=|z1−z2|
    Barg(z−z1)=arg(z−z2)
    C∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0
    Darg(z−z1)=arg(z2−z1)

  • Let Z1 and Z2 are two non-zero complex number such that |Z1+Z2|=|Z1|=|Z2|, then Z1Z2 may be :

    A1+ω
    B1+ω2
    Cω
    Dω2