Question

The complex numbers ${\displaystyle z=x+iy}$ which satisfy the equation ${\displaystyle \left|\frac{z-5i}{z+5i}\right|=1}$ lie on (a) The x-axis (b) The straight line ${\displaystyle y=5}$ (c) A circle passing through the origin (d) Non of these

Options

A. the X-axis
B. the straight line y=5
C. a cicle passing through the origin
D. None of these

Answer

A

Explanation

Given ,`|(z-5i)/(z+5i)| =1 rArr|z-5i|=|z+5i|`
`[because if |z-z_1|=|z-z_2|` then it is perpendicular bisector of `z_1 and z_2`]

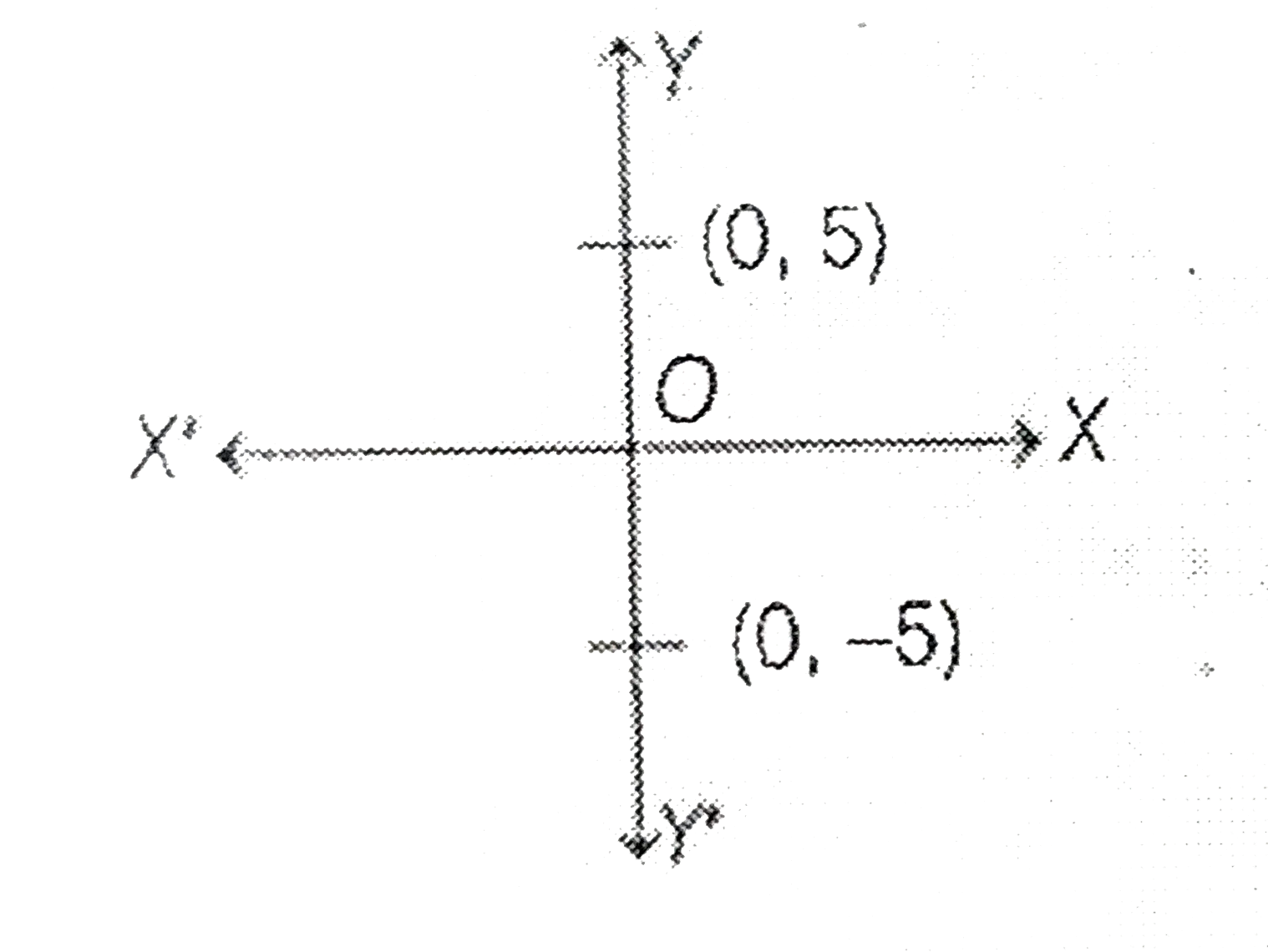
`because` Perpendicular bisector (0,5) and (0,-5) is x- axis