ABC एक त्रिभुज है जिसमे AC और AB पर खिचे गए शीर्षलम्ब BE और CF बराबर है ( देखिए आक्रति ) | दर्शाइए कि- (i) ΔABE ~-= ΔACF
(ii) AB -= AC, अर्थात ΔABC एक समद्धिबाहू त्रिभुज है |
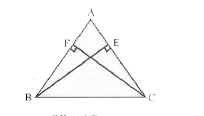
The correct Answer is:AB -= AC
Step by step video, text & image solution for ABC एक त्रिभुज है जिसमे AC और AB पर खिचे गए शीर्षलम्ब BE और CF बराबर है ( देखिए आक्रति ) | दर्शाइए कि- (i) DeltaABE ~-= DeltaACF (ii) AB -= AC, अर्थात DeltaABC एक समद्धिबाहू त्रिभुज है | by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.35videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.46videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.17videos
त्रिभुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - चतुर्भुज EXERCISE - प्रश्नावली 8.2 पर आधारित अभ्यास प्रश्न7videos
चतुर्भुज
- BOOK - SCIENCE PUBLICATIONCHAPTER - दो चरों वाले रैखिक समीकरणEXERCISE - प्रश्नावली 4.4 पर आधारित अभ्यास प्रश्न1videos
दो चरों वाले रैखिक समीकरण
Similar Questions
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्धिबाहू त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है | (देखिए आक्रति ) | यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि-
(i) ΔABD ~-= ΔACD
(ii) ΔABP ~-= ΔACP
(iii) AP कोण A और कोण D दोनों को समद्धिभाजित करता है |
(iv) AP रेखाखण्ड BC का लम्ब समद्धिभाजक है |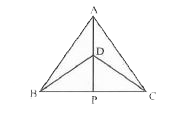
02:11View Solutionदर्शाइए क समकोण त्रिभुज में कोण सबसे लम्बी भुजा होती है |
02:46View Solutionचतुर्भुज ACBD में, AC -= AD है और AB कोण A को सम्द्धिभाजिक कहेते है (देखिए आकृति) | दर्शाइए कि ∠ABC -= ∠ABD है |
BC और BD के बारे में आप क्या कह सकते है ?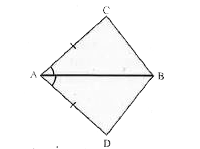
02:45View SolutionP, Q और R क्रमशः एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य बिन्दु है। सिद्ध कीजिए कि ΔPQR भी एक समबाहु त्रिभुज हैं।
02:17View Solutionनिम्नलिखित समीकरणों को (i) संख्या रेखा और तथा (ii) कार्तिए तल पर प्रदर्शित कीजिए।
(a) x−2=0 " (b)2x+4=3x+1
(c) y+5=005:41View SolutionDetermine the point of symmetry of a regular hexagon.
02:10View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
02:17View SolutionMatch the following Column A to Column B
02:10View SolutionMatch the following Column A to Column B
01:13View SolutionMatch the following Column A to Column B
03:12View SolutionThe inequation represented by the graph given below is :
05:46View SolutionThe inequation that best describes the graph given below is _________
05:06View SolutionThe inequation that best describes the following graph is _________
04:26View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt04:37View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt03:18View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt04:17View Solution