Four equal charges of value +Q are placed at any four vertices of a regular hexagon of side a. By suitably choosing the vertices, what can be the maximum possible magnitude of electric field at the centre of the hexagon?
(A) Q4π∈0a2
(B) √2Q4π∈0a2
(C) √3Q4π∈0a2
(D) 2Q4π∈0a2
Q4πε0a2
√2Q4πε0a2
√3Q4πεa2
2Q4πε0a2
The correct Answer is:c
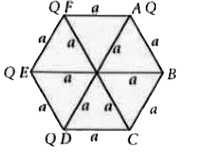
To maximize the elctric field at the centre both charges should be placed at adjecent vertices.
Net field due to charge at A and D is zero here.
Total System of electric field due to the charges is
∴Etotal=√E2F+E2E+2EFEEcos60∘
=√2E2+2E2×12 (∵EF=EE=E)
=√2E2+E2=√3E2orEtotal=√3E
So , maximum electric field is
Etotal=√3×14πε0Qa2 (using(i))
Topper's Solved these Questions
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE Previous Years Questions ) CATEGORY 2 : Single Option correct Type
Explore 8 Videos
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE Previous Years Questions ) CATEGORY 3 : One or More than One Opion correct Type
Explore 4 Videos
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE / WORKOUT )CATEGORY 3 : One or More than One Option Correct Type (2 Marks)
Explore 10 Videos
- ELECTROMAGNETIC WAVES Book:MTG-WBJEEChapter:ELECTROMAGNETIC WAVES Exercise:WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
Explore 10 Videos
- GRAVITATIONBook:MTG-WBJEEChapter:GRAVITATIONExercise:WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
Explore 7 Videos
Similar Questions
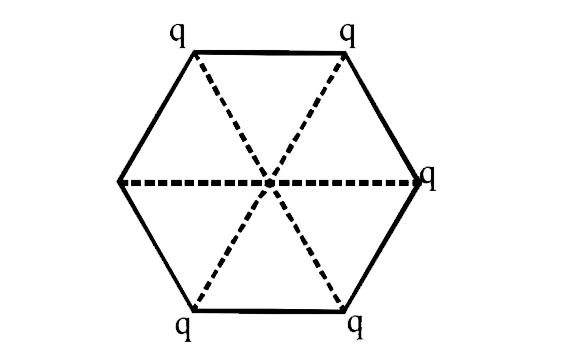
Five point charges, each of value +q are placed on five vertices of a regular hexagon of side Lm. What is the magnitude of the force on a point charge of value -q coulomb placed at the centre of the hexagon?
View SolutionFive point charges, each of value +q coul, are placed on five vertices of a regular hexagon of isde L meters. The magnitude of the force on the point charge of value -q coul, placed at the centre of the hexagen is…………….
View Solution
Knowledge Check
Five point charges, +q each are placed at the five vertices of a regular hexagon. The distance of the center of the hexagon from any fo the vertices is a. the electric field at the center of the hexagon is
Aq4πε0a2Bq8πε0a2Cq16πε0a2DzeroFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq2πε0a2C5q4πε0a2D5q2πε0a2
Five point charges, each +q are placed on five vertices of a regular hexagon of side' l '. Find the magnitude of the resultant force on a charge –q placed at the centre of the hexagon.
View SolutionFour equal charges each 16μC are placed on four corners of a square of side 0.4m. Calculate force on q is zero, how are Q and q related ?
View SolutionFour identical point charges, each of charge q, are placed on the vertices of a regular hexagon of side a such that the net electric field at centre of hexagon is zero. If one of the charge is now removed, then the electric field at centre of hexagon is k- 4.60
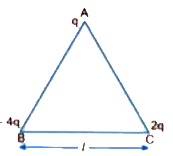
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.

View SolutionThree point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
View Solution

