A pendulum bob of mass m = 80 mg, carrying a charge of q=2×10−8C, is at rest in a horizontal, uniform electric field of E = 20,000 V/m. The tension T in the thread of the pendulum and the angle α it makes with vertical, is (take g=9.8m/s2)
3.92×10−8,72∘
7.84×10−6,90∘
8.8×10−4,27∘
1.96×10−4,18∘
The correct Answer is:c
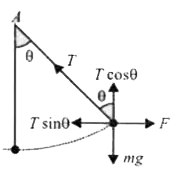
the different forces acting on the pendulum bob are :
(i) Weight of the bob , mg
(ii) Tension in the thread of the bob , T and
(iii) Force on the charged charged bob due to the electric field, F . Here , Mass of the bob ,
m=80mg=80×10−6kg
Charge on the bob,
q=2×10−8 coulomb Electric field,
E=20,000V/m
∴F=qE=2×10−8×20,000N
Let the thread makes an angle θ with the vertical at its equilibrium position.
Horizontal and vertical force balances of the bob give
Tsinθ=F and Tcosθ=mg ..(ii)
Dividing (i) by (ii) , we get
tanθ=Fmg=2×10−8×20,00080×10−6×9.8[takingg=9.8m/s2]
=0.51
∴θ=tan−1(0.51)=27∘
From (ii) , we have
T=mgcosθ=80×10−6×9.8cos27∘=8.8×10−4N
Therefore , the tension in the thread is 8.8×10−4 N and it makes an angle 27∘ with the vertical
Topper's Solved these Questions
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE Previous Years Questions ) CATEGORY 1 : Single Option correct Type
Explore 23 Videos
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:(WB JEE Previous Years Questions ) CATEGORY 2 : Single Option correct Type
Explore 8 Videos
- ELECTROSTATICSBook:MTG-WBJEEChapter:ELECTROSTATICSExercise:WB JEE / WORKOUT) CATEGORY 2 : Single Option Correct Type (2 Marks)
Explore 15 Videos
- ELECTROMAGNETIC WAVES Book:MTG-WBJEEChapter:ELECTROMAGNETIC WAVES Exercise:WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
Explore 10 Videos
- GRAVITATIONBook:MTG-WBJEEChapter:GRAVITATIONExercise:WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
Explore 7 Videos
Similar Questions
A pendulum bob of mass 80mg and carrying a charge of 2×10−8C is at rest in a uniform, horizontal electric field of 20k Vm−1. Find the tension in the thread.
View SolutionA pendulum bob of mass 80mg and carrying a charge of 2×10−4 coulomb is at rest in a uniform horizontal electric field of 20kVm.The tension in the thread of the pendulum is x times10−4 N.Find value of x?
View Solution
Knowledge Check
A pendulum bob of mass 30.7×10−6kg and carrying a chargee 2×10−8C is at rest in a horizontal uniform electric field of 20000V/m. The tension in the thread of the pendulum is (g=9.8m/s2)
A3×104NB4×10−4NC5×10−4ND6×10−4NThe bob of a simple pendulum has mass 2g and a charge of 5.0μC. It is at rest in a uniform horizontal electric field of intensity 2000V/m. At equilibrium, the angle that the pendulum makes with the vertical is: (take g=10m/s2)
Atan−1(2.0)Btan−1(0.2)Ctan−1(5.0)Dtan−1(0.5)A pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
AmgsinθBmgCqEsinθDqEcosθ
A pendulum bob of mass 80 mg and carrying charge of 3×10−8C is placed in an horizontal electric field. It comes to equilibrium position at an angle of 37∘ with the vertical. Calculate the intensity of electric field. (g = 10m/s2 )
View SolutionA uniform electric field of 3×104 N/C is applied iin a horizontal direction . A pendulum bob of mass 90 mg and carrying a charge of 1.5×10−8 C is suspended through a string of length 1m. Calculate tension developed in the string and the angle made by the string with the vertical .
View SolutionA simple pendulum with a bob of mass m=1 kg, charge q=5μC and string length imis given a horizontal velocity a in a uniform electric field E=2×106Vm at its bottommost point A, as shown in figure. It is given that the speed a is such that the particle leaves the circle at point C. Find the speed a (Take g=10ms2)
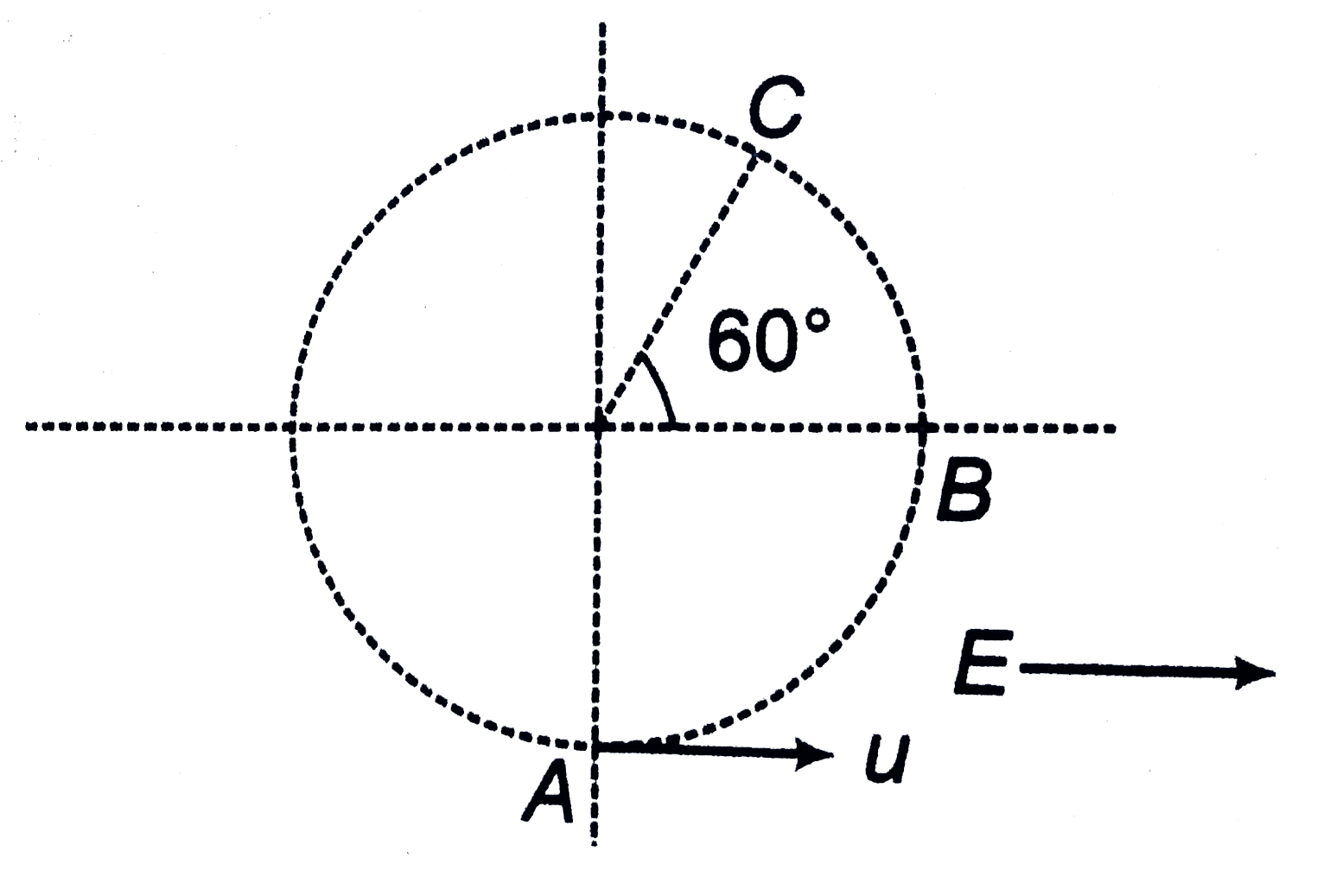
View SolutionThe bob of a pendulum of mass 8μg carries an electric charge of 39.2×10−10 coulomb in an electric field of 20×103 volt/meter and it is at rest. The angle made by the pendulum with the vertical will be
View SolutionWhat is the velocity of the bob of a simple pendulum at its mean position, if it is able to rise to vertical height of 10 cm (take g=9.8m/s2)
View Solution

