Find the area of the shaded region in Fig where ABCD is a square of side 14 cm.
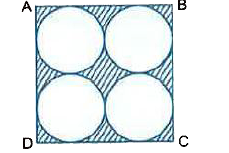
The correct Answer is:Are of shaded region = 42cm2
Step by step video, text & image solution for Find the area of the shaded region in Fig where ABCD is a square of side 14 cm. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MODEL QUESTION PAPER - 9 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 9 [UNSOLVED]EXERCISE - SECTION - C
10 Videos
- MODEL QUESTION PAPER - 1 BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER - 1 EXERCISE - SECTION - C
15 Videos
- MODEL QUESTION PAPER -2 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -2 [UNSOLVED]EXERCISE - SECTION-D
10 Videos
Similar Questions
Find the area of the shaded region in figure where ABCD is a square of side 14 cm.

View SolutionFind the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
View SolutionFind the area of the shaded region in Fig. 15.48, where ABCD is a square of side 10 cm. (Use π=3.14) (FIGURE)
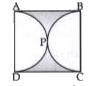
View SolutionFind the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
View SolutionIn the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and al circles are of the same diameter.

View SolutionFind the area of the shaded region in Fig. 15.49, if ABCD is a square of side 14 cm and APD and BPC are semi-circles. (FIGURE)
View SolutionFind the area of the shaded region in figure, if ABCD is a square of side 7 cm. and APD and BPC are semi-circles
View SolutionFind the area of the shaded design in Fig. 12.17, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square asdiameter.
View SolutionFind the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.
View SolutionFind the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
View Solution
