In fig height of a building is h+2 and point C is h m from the foot of the building. Find the angle of elevation of the top of the building from a point 2 m from point C.
The correct Answer is:45∘
To solve the problem step by step, we will analyze the given information and apply trigonometric principles.
Step 1: Understand the problem
We have a building with a height of h+2 meters. Point C is located h meters from the foot of the building, and we need to find the angle of elevation (let's call it θ) from point D, which is 2 meters away from point C.
Step 2: Identify the distances
- The height of the building (AB) = h+2 meters.
- Distance from the foot of the building to point C (BC) = h meters.
- Distance from point C to point D (CD) = 2 meters.
- Therefore, the total distance from the foot of the building to point D (BD) = BC + CD = h+2 meters.
Step 3: Set up the tangent function
Using the definition of the tangent function in a right triangle:
tan(θ)=OppositeAdjacent
Here, the opposite side is the height of the building (AB = h+2) and the adjacent side is the distance from the foot of the building to point D (BD = h+2).
Step 4: Write the equation
Substituting the values into the tangent function:
tan(θ)=h+2h+2
This simplifies to:
tan(θ)=1
Step 5: Find the angle
We know that tan(45∘)=1, therefore:
θ=45∘
Conclusion
The angle of elevation of the top of the building from point D is 45∘.
We have a building with a height of h+2 meters. Point C is located h meters from the foot of the building, and we need to find the angle of elevation (let's call it θ) from point D, which is 2 meters away from point C.
- The height of the building (AB) = h+2 meters.
- Distance from the foot of the building to point C (BC) = h meters.
- Distance from point C to point D (CD) = 2 meters.
- Therefore, the total distance from the foot of the building to point D (BD) = BC + CD = h+2 meters.
Using the definition of the tangent function in a right triangle:
tan(θ)=OppositeAdjacent
Here, the opposite side is the height of the building (AB = h+2) and the adjacent side is the distance from the foot of the building to point D (BD = h+2).
Substituting the values into the tangent function:
tan(θ)=h+2h+2
This simplifies to:
tan(θ)=1
We know that tan(45∘)=1, therefore:
θ=45∘
The angle of elevation of the top of the building from point D is 45∘.
Topper's Solved these Questions
- HEIGHT AND DISTANCEBook:VK GLOBAL PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:PROFICIENCY EXERCISE ( SHORT ANSWER QUESTIONS II)
Explore 32 Videos
- HEIGHT AND DISTANCEBook:VK GLOBAL PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:PROFICIENCY EXERCISE ( LONG ANSWER QUESTIONS II)
Explore 11 Videos
- HEIGHT AND DISTANCEBook:VK GLOBAL PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:PROFICIENCY EXERCISE ( VERY SHORT ANSWER QUESTIONS I)
Explore 12 Videos
- COORDINATE GEOMETRY Book:VK GLOBAL PUBLICATIONChapter:COORDINATE GEOMETRY Exercise:SELF-ASSESSMENT TEST
Explore 10 Videos
- INTRODUCTION TO TRIGONOMETRYBook:VK GLOBAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRYExercise:SELF - ASSESSMENT TEST
Explore 9 Videos
Similar Questions
From a point P on the ground the angle of elevation of a 10m tall building is 30o . A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45o . Find the length of the flag-staff and the distance of the building from the point P . (Take √3=1.732) .
View SolutionFrom a point P on the ground the angle of elevation of the top of a 10 m tall building is 30∘. A flag is hoisted at the top of building and the angle of elevation of the top of the flagstaff from P is 45∘. Find the length of the flagstaff and the distance of the building from the point? (You may take √3=1.732)
View Solution
Knowledge Check
At a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
A25√3mB25mC√3mD√3/25mFrom a point P on the ground the angle of elevation of the top of a 10 m tall building is 30∘. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45∘. Find the length of the flagstaff
A5.2mB8.32mC6.2mD7.32mFrom a point A on the ground, the angle of elevation of the top of a 20 m tall buiding is 45∘. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60∘. Find the length of the flag staff and the distance of the building from the point A.
A20 m , 15 mB20m, 14.64 mC25 m , 15mD20 m, 19m
From a point P on the ground the angle of elevation of the top of a 10 m tall building is 30∘ . A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45∘ . Find the length of the flagstaff . (Take √3=1.732)
View SolutionTwo points P and Q are at the distance of x and y (where y>x) respectivelyf from the base of a building and on a straight line.If the angles of elevation of the top of the building from points P and Q are complementary ,then what is the height of the building ?
View SolutionEshan purchased a new building for her business. Being in the prime location, she decided to make some more money by putting up an advertisement sign for a rental ad income on the roof of the building.
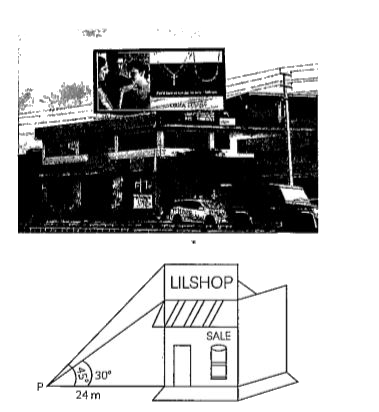
From a point P on the ground level, the angle of elevation of the roof of the building is 30∘ and the angle of elevation of the top of the sign board is 45∘. The point P is at a distance of 24 m from the base of the building.
If the point of observation P is moved 10 m towards the base of the building, then the angle of elevation θ of the roof of the building is given by
View SolutionEshan purchased a new building for her business. Being in the prime location, she decided to make some more money by putting up an advertisement sign for a rental ad income on the roof of the building.
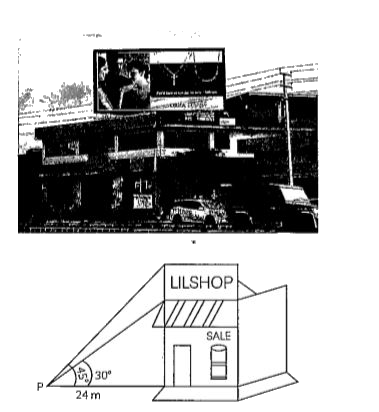
From a point P on the ground level, the angle of elevation of the roof of the building is 30∘ and the angle of elevation of the top of the sign board is 45∘. The point P is at a distance of 24 m from the base of the building.
On the basis of the above information, answer any four of the following questions:
The distance of the point P from the top of the sign board, is
View SolutionEshan purchased a new building for her business. Being in the prime location, she decided to make some more money by putting up an advertisement sign for a rental ad income on the roof of the building.
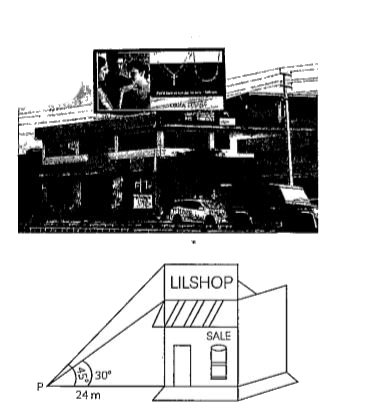
From a point P on the ground level, the angle of elevation of the roof of the building is 30∘ and the angle of elevation of the top of the sign board is 45∘. The point P is at a distance of 24 m from the base of the building.
The height of the building (without the sign board) is
View Solution

