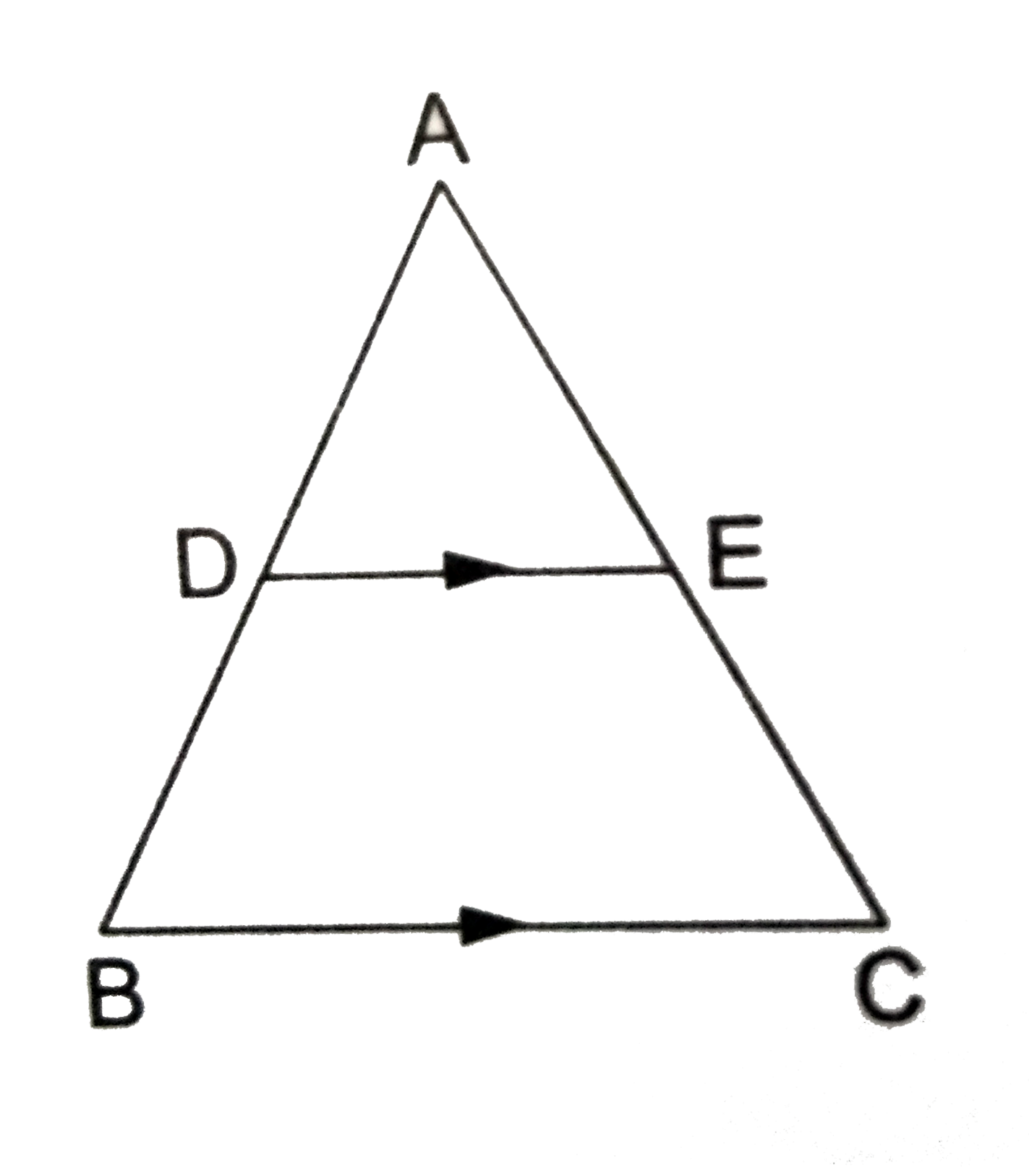
In ΔABC,DE||BC. If AD= 2.4 cm, AE= 3.2 cm, DE= 2 cm and BC= 5 cm, find BD and CE.
The correct Answer is:BD=3.6 cm,CE=4.8 cm
To solve the problem, we will use the properties of similar triangles since DE is parallel to BC. Let's break down the solution step by step.
Step 1: Understand the given information
We have triangle ABC with DE parallel to BC. The lengths provided are:
- AD = 2.4 cm
- AE = 3.2 cm
- DE = 2 cm
- BC = 5 cm
We need to find the lengths of BD and CE.
Step 2: Set up the proportion using similar triangles
Since DE is parallel to BC, triangles ADE and ABC are similar. Therefore, we can set up the following proportion:
ADAB=DEBC
Let BD = x and CE = y. Then, we can express AB and AC in terms of x and y:
- AB = AD + BD = 2.4 + x
- AC = AE + CE = 3.2 + y
Step 3: Substitute the known values into the proportion
Substituting the known values into the proportion gives us:
2.42.4+x=25
Step 4: Cross-multiply to solve for x
Cross-multiplying yields:
2.4⋅5=2⋅(2.4+x)
This simplifies to:
12=4.8+2x
Step 5: Solve for x
Now, isolate x:
12−4.8=2x
7.2=2x
x=7.22=3.6 cm
So, BD = 3.6 cm.
Step 6: Find CE using another proportion
Now, we can use the other proportion to find CE:
AEAC=DEBC
Substituting the known values gives us:
3.23.2+y=25
Step 7: Cross-multiply to solve for y
Cross-multiplying yields:
3.2⋅5=2⋅(3.2+y)
This simplifies to:
16=6.4+2y
Step 8: Solve for y
Now, isolate y:
16−6.4=2y
9.6=2y
y=9.62=4.8 cm
So, CE = 4.8 cm.
Final Answer
Thus, the lengths are:
- BD = 3.6 cm
- CE = 4.8 cm
---
We have triangle ABC with DE parallel to BC. The lengths provided are:
- AD = 2.4 cm
- AE = 3.2 cm
- DE = 2 cm
- BC = 5 cm
Since DE is parallel to BC, triangles ADE and ABC are similar. Therefore, we can set up the following proportion:
- AB = AD + BD = 2.4 + x
- AC = AE + CE = 3.2 + y
Substituting the known values into the proportion gives us:
Cross-multiplying yields:
Now, isolate x:
7.2=2x
x=7.22=3.6 cm
Now, we can use the other proportion to find CE:
Cross-multiplying yields:
Now, isolate y:
9.6=2y
y=9.62=4.8 cm
Thus, the lengths are:
- BD = 3.6 cm
- CE = 4.8 cm
Topper's Solved these Questions
- TRIANGLESBook:VK GLOBAL PUBLICATIONChapter:TRIANGLESExercise:PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)
Explore 15 Videos
- TRIANGLESBook:VK GLOBAL PUBLICATIONChapter:TRIANGLESExercise:SELF ASSESSMENT TEST
Explore 10 Videos
- TRIANGLESBook:VK GLOBAL PUBLICATIONChapter:TRIANGLESExercise:PROFICIENCY EXERCISE (VERY SHORT ANSWER QUESTIONS)
Explore 14 Videos
- REAL NUMBERSBook:VK GLOBAL PUBLICATIONChapter:REAL NUMBERSExercise:Self -Assessment Test
Explore 11 Videos
- VALUE-BASED QUESTIONSBook:VK GLOBAL PUBLICATIONChapter:VALUE-BASED QUESTIONSExercise:Unit-VII : (Statistics & Probability)
Explore 8 Videos
Similar Questions
Knowledge Check
In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cm
In the given figure, if ∠ADE=∠B, show that ΔADE~ΔABC. If AD=3.8cm,AE=3.6cm,BE=2.1cm,andBC=4.2cm, find DE.
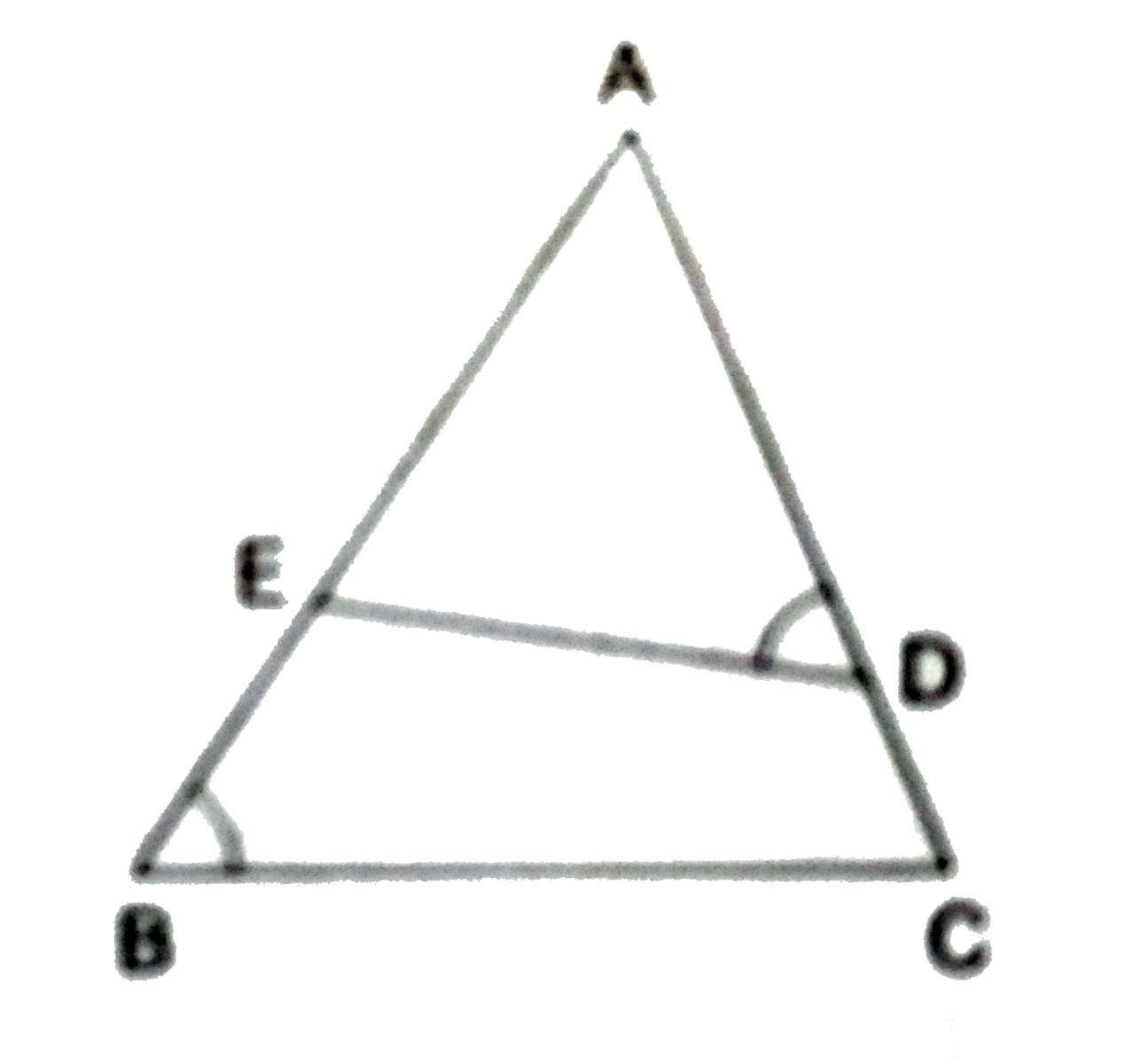
View SolutionIn ΔABC,DE∣∣BC so that AD==2.4cm,AE=3.2cmandEC=4.8cm, then , AB= ?
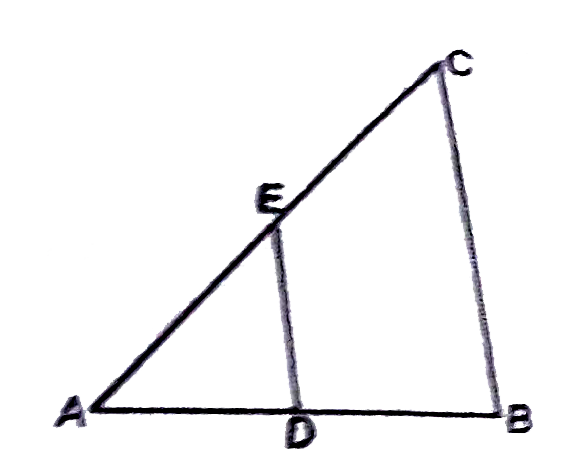
View SolutionIn the figure △ABC~△AED. If AD=5 cm , AE= 6 cm, BC= 12 cm and AB = 15 cm. Determine AC and DE.
View SolutionΔABC~ΔDEF. If AB= 4cm,BC = 3.5cm,CA = 2.5cmandDF = 7.5cm, then find perimeter of ΔDEF.
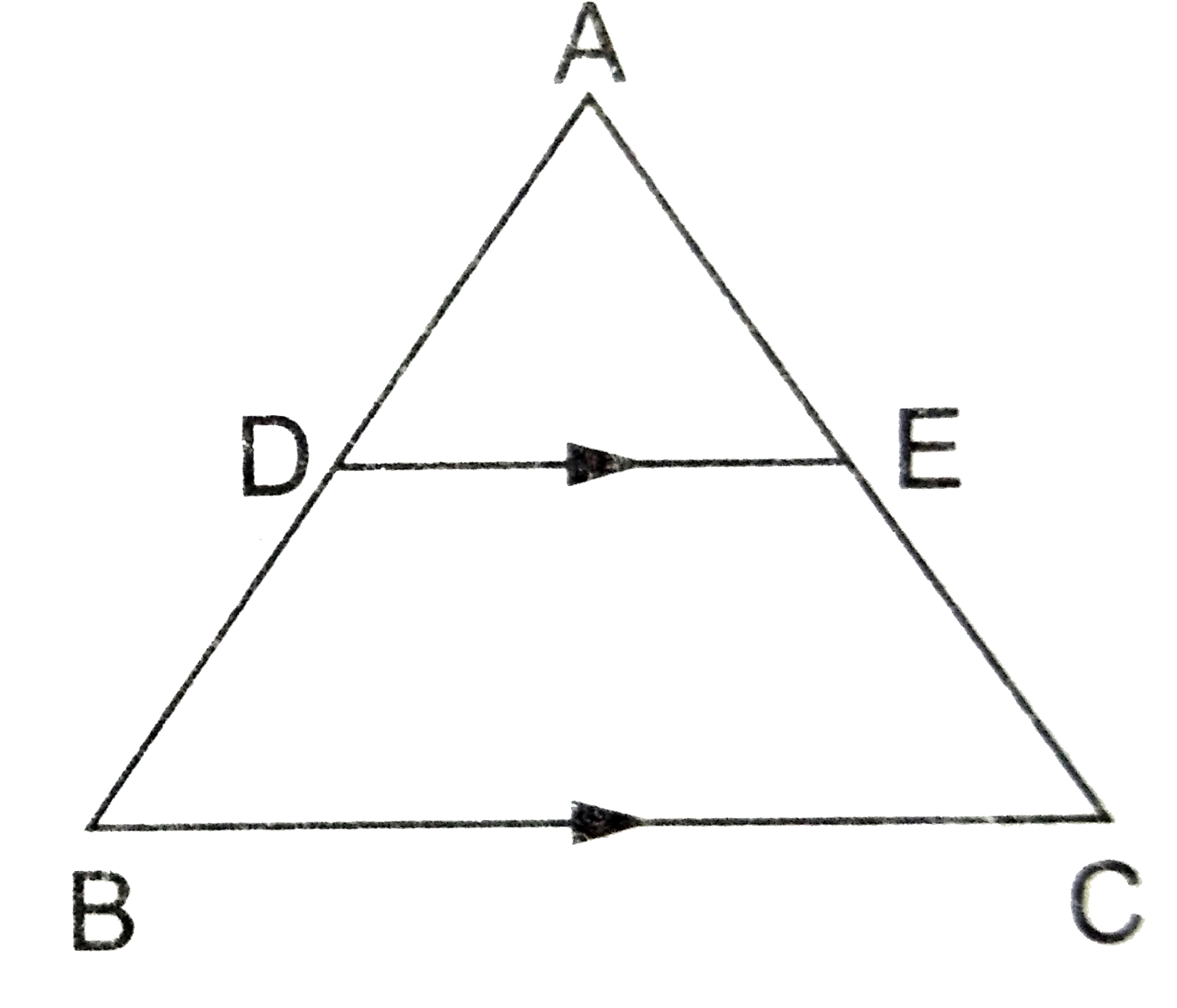
View SolutionIn ΔABC,DE∣∣BC so that AD=(7x−4)cm,AE=(5x−2)cm,DB=(3x+4)cmandEC=3x. Then, we have
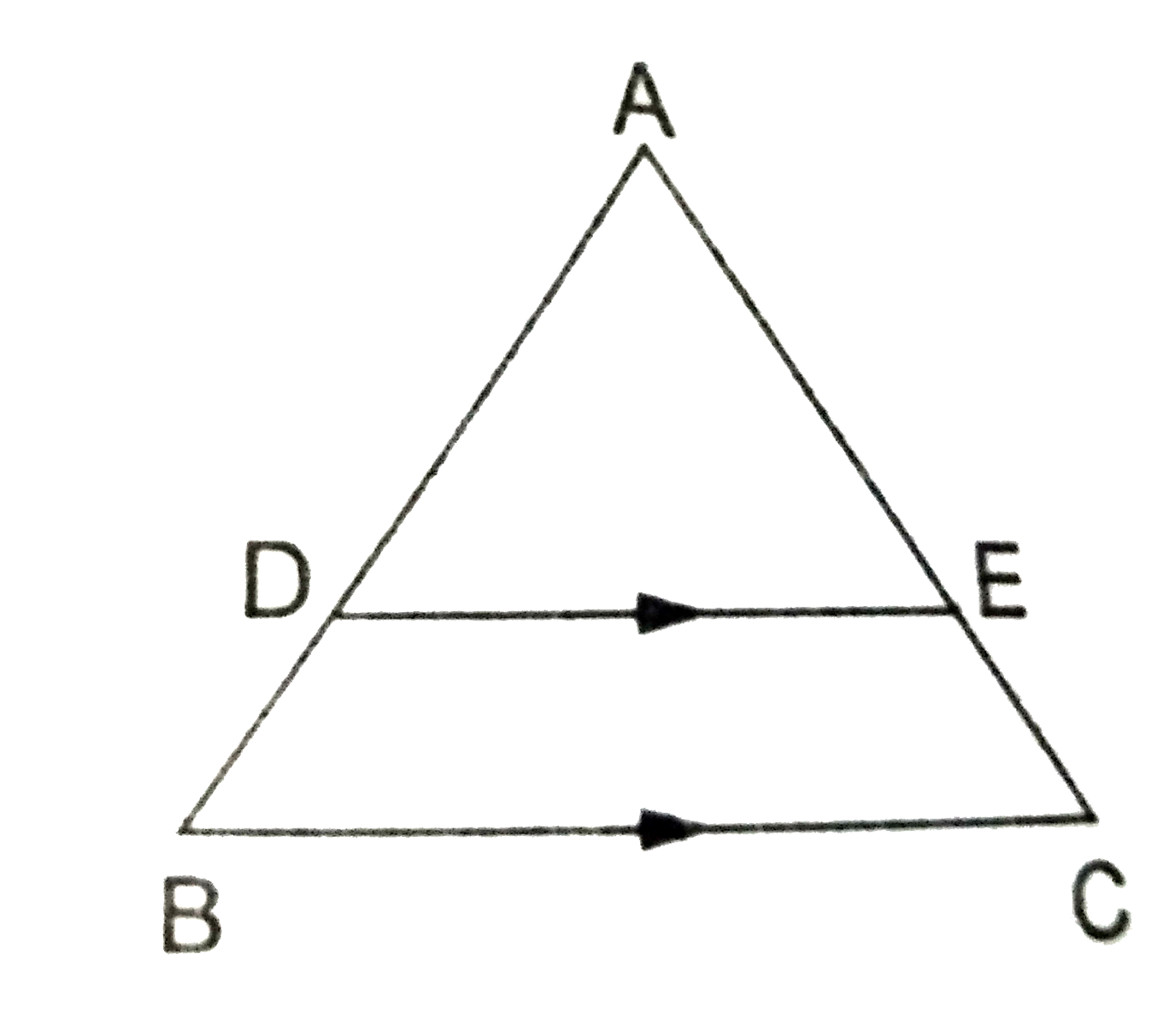
View SolutionΔABC~ΔDEF such that DE = 3 cm , EF = 2 cm , DF = 2.5 and BC = 4 cm . Find the perimeter of ΔABC.
View SolutionIn the given figure, DE|∣|BC,AD=2cm,BD=2.5cm,AE=3.2cmandDE=4cm. Find AC and BC.
View Solution


