A circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
The correct Answer is:True OQ>OP
Step by step video, text & image solution for A circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - PROFICIENCY EXERCISE ( Long Answer Questions )
18 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - PROFICIENCY EXERCISE (Very Short Answer Questions)
12 Videos
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF - ASSESSMENT TEST
11 Videos
- HEIGHT AND DISTANCEBOOK - VK GLOBAL PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - SELF ASSESSMENT TEST
11 Videos
Similar Questions
Knowledge Check
The point (5,−7) lies outside the circle
Ax2+y2−8x=0Bx2+y2−5x+7y=0Cx2+y2−5x+7y−1=0Dx2+Y2−8x+7y−2=0Point (0,−8) lies
Ain the II quadrantBin the IV quadrantCon the x-axisDon the y-axisThe centre of the circle is at the origin and its radius is 10. Which of the following points lies inside the circle?
A(6,8)B(0, 11)C(-10,0)D(7,7)
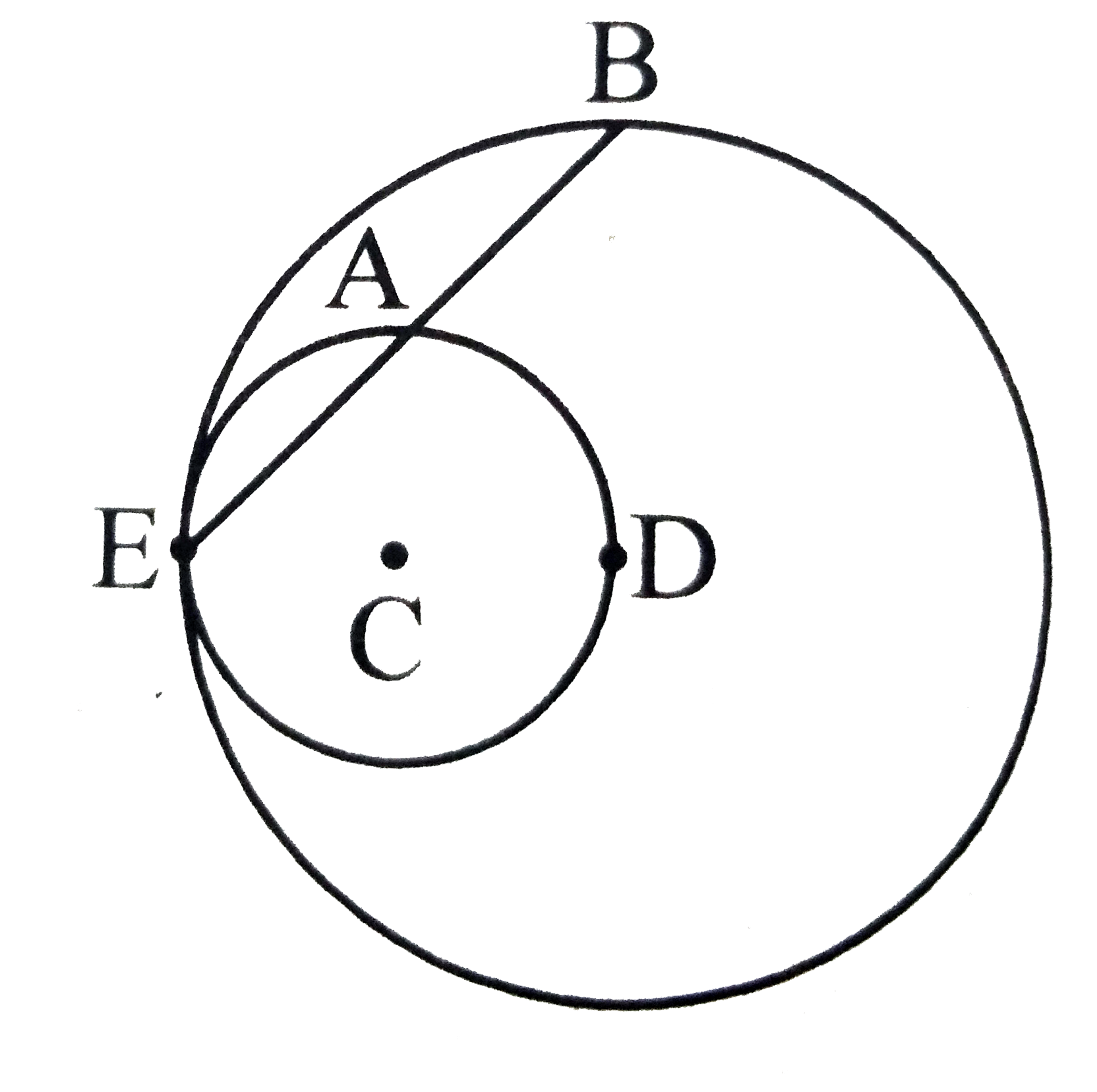
In the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
View SolutionThe point (-a, - a) lies on the circle passing through the origin and the point of intersection of the straight line x+y+a=0 with the circle x2+y2=a2
View SolutionIn the xy plane, the segment with end points (3,8) and (-5,2) is the diameter of the circle. The point (k,10) lies on the circle for
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionIf 3x+y=0 is a tangent to a circle whose center is (2,−1) , then find the equation of the other tangent to the circle from the origin.
View Solution
