A Bohr's hydrogen atom undergoes a transition $n = 5 \to n = 4$ and emits a photon of frequency $f$ . Frequency of circular motion of electron in $n = 4 or b i t i s f_{4}$ . The ratio $f / f_{4}$ is found to be $18 / 5 m$ . State the value of $m$ .

A

4

B

2

C

5

D

1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$E_{n} = - \frac{m Z^{2} e^{4}}{8 ε_{0}^{2} n^{2} h^{2}}$ ,
so, $h f = + \frac{m Z^{2} e^{4}}{8 ε_{0}^{2} h^{2}} [\frac{1}{16} - \frac{1}{25}]$
$∴ f = \frac{m Z^{2} e^{4}}{8 ε_{0}^{2} h^{3}} [\frac{9}{16 \times 25}] \dots(i)$
and frequency $f_{4} = \frac{Z^{2} e^{4} m}{4 ε_{0}^{2} n^{3} h^{3}} = \frac{Z^{2} e^{4} m}{4 ε_{0}^{2} {(4)}^{3} h^{3}} ...(ii)$
$∴ f / f_{4} = 18 / 25$ , so m = 5

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If in hydrogen atom, radius of $n^{t h}$ Bohr orbit is $r_{n}$ ., frequency of revolution of electron in $n^{t h}$ orbit is $f_{n}$ choose the correct option.
A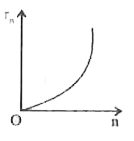
B
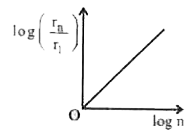C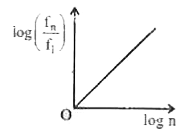
DBoth (a) and (b)
Question 2 - Select One
If in hydrogen atom, radius of $n^{t h}$ Bohr orbit is , $n_{r}$ frequency of revolution of electron in $n^{t h}$ orbit is $f_{n}$ choose the correct option
A
B
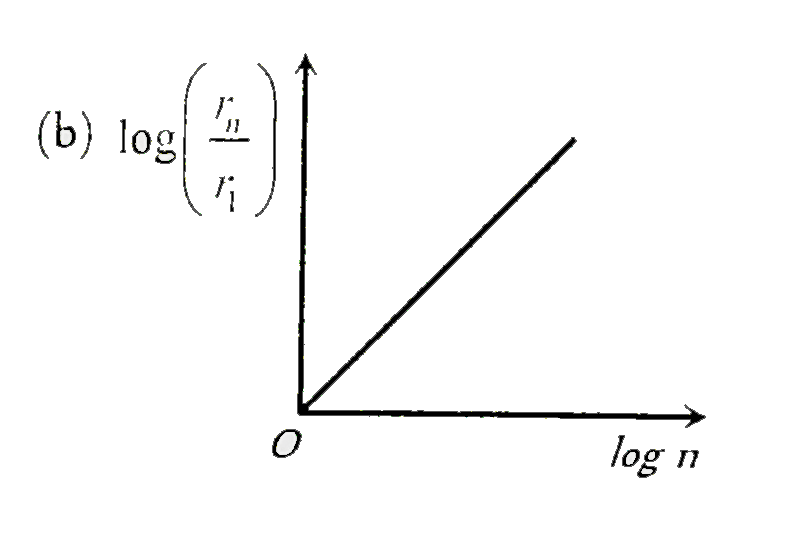C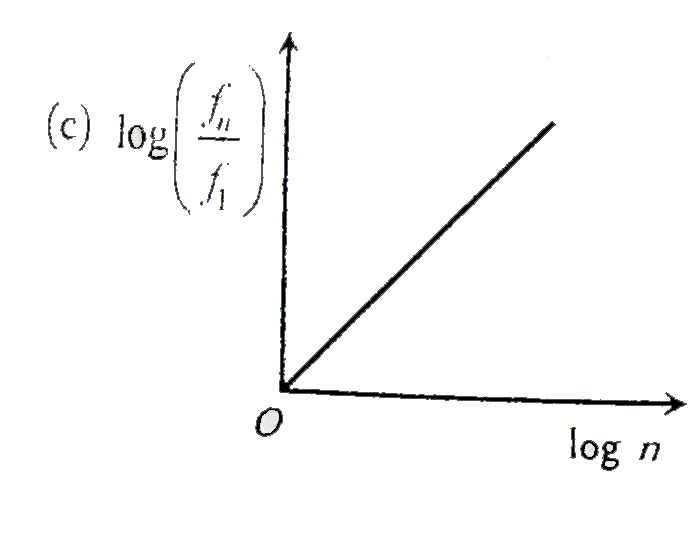
DBoth (a) and (b)
Question 3 - Select One
In hydrogen atom electron jumps from $(n + 1) t h$ state to $n t h$ state the frequency of emitted photon is directly proportional to $(n ⟩ 1)$
A $n$
B $\frac{1}{n}$
C $\frac{1}{n^{2}}$
D $\frac{1}{n^{3}}$

MTG-WBJEE-ATOMIC PHYSICS-WBJEE WORKOUT (CATEGORY 2 : Single Option Correct Type )

Home
Ask Doubt
Profile