Two capacitors C1=2mFandC2=8mF are seperately charged from the same battery. These two capacitors are then allowed to discharge separately through resistors of same resistance with a switch in series which are kept open initially. Both switches are closed at t = 0.
Current at t = 0 will be zero in both the capacitors.
At t = 0 current in C1 will be 4 times the current in C2.
At t = 0 current in both the capacitors will be the same
Capacitor C1 loses 25% of its initial charge in lesser time than capacitor C2.
The correct Answer is:C, D
To solve the problem step by step, we will analyze the discharge of the capacitors and the relationships between their charge, current, and time constants.
Step 1: Understand the Initial Conditions
- We have two capacitors:
- C1=2mF=2×10−3F
- C2=8mF=8×10−3F
- Both capacitors are charged from the same battery, so they have the same initial voltage V.
Step 2: Calculate the Initial Charge on Each Capacitor
The charge Q on a capacitor is given by the formula:
Q=C⋅V
- For C1:
Q1=C1⋅V=2×10−3⋅V
- For C2:
Q2=C2⋅V=8×10−3⋅V
Step 3: Write the Discharge Equation
The charge on a capacitor discharging through a resistor is given by:
Q(t)=Q0e−tRC
Where:
- Q0 is the initial charge.
- R is the resistance.
- C is the capacitance.
Step 4: Analyze the Current Flow
The current I through the capacitor can be expressed as:
I(t)=−dQdt=Q0Re−tRC
At t=0:
- The initial current I0 for both capacitors is:
I0=VR
Since both capacitors are charged to the same voltage and have the same resistance, the initial current will be the same for both capacitors.
Step 5: Compare Time Constants
The time constant τ for a capacitor is given by:
τ=R⋅C
- For C1:
τ1=R⋅C1=R⋅2×10−3
- For C2:
τ2=R⋅C2=R⋅8×10−3
Since C1<C2, we have τ1<τ2. This means C1 will discharge faster than C2.
Step 6: Determine Charge Loss
To find out how long it takes for C1 to lose 25% of its charge:
- The final charge after losing 25%:
Qf=Q1−0.25Q1=0.75Q1
Using the discharge equation:
0.75Q1=Q1e−tτ1
This simplifies to:
0.75=e−tτ1
Taking the natural logarithm:
−tτ1=ln(0.75)
Thus:
t=−τ1ln(0.75)
Conclusion
Since τ1<τ2, C1 will lose 25% of its charge in a shorter time than C2.
- We have two capacitors:
- C1=2mF=2×10−3F
- C2=8mF=8×10−3F
- Both capacitors are charged from the same battery, so they have the same initial voltage V.
The charge Q on a capacitor is given by the formula:
Q=C⋅V
- For C1:
Q1=C1⋅V=2×10−3⋅V
- For C2:
Q2=C2⋅V=8×10−3⋅V
The charge on a capacitor discharging through a resistor is given by:
Q(t)=Q0e−tRC
Where:
- Q0 is the initial charge.
- R is the resistance.
- C is the capacitance.
The current I through the capacitor can be expressed as:
I(t)=−dQdt=Q0Re−tRC
At t=0:
- The initial current I0 for both capacitors is:
I0=VR
Since both capacitors are charged to the same voltage and have the same resistance, the initial current will be the same for both capacitors.
The time constant τ for a capacitor is given by:
τ=R⋅C
- For C1:
τ1=R⋅C1=R⋅2×10−3
- For C2:
τ2=R⋅C2=R⋅8×10−3
To find out how long it takes for C1 to lose 25% of its charge:
- The final charge after losing 25%:
Qf=Q1−0.25Q1=0.75Q1
Using the discharge equation:
0.75Q1=Q1e−tτ1
This simplifies to:
0.75=e−tτ1
Taking the natural logarithm:
−tτ1=ln(0.75)
Thus:
t=−τ1ln(0.75)
Since τ1<τ2, C1 will lose 25% of its charge in a shorter time than C2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS BASED ON A GIVEN PASSAGE/COMPREHENSION)
Explore 15 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS ASSERTION REASON TYPE QUESTIONS)
Explore 10 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (ADVANCED) FOR IIT ENTRANCE)
Explore 9 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A capacitor C1 of capacitance 1μF and a capacitor C2 of capacitance 2μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t=0.
View SolutionA capacitor of capacitance 500(μ)Fis connected to a battery through a (10k(Ω)) resistor.The charge stored on the capacitance 2(μ)F are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors.Both the discharge circuits are connected at t=0.
View Solution
Knowledge Check
Capacitors C1=1μF and C2=2μF are separately charged from the same battery. They are allowed to discharge separately through equal resistors
AThe currents in the two dicharging circuits at t=0 is zeroBThe currents in the two discharging circuits at t=0 are equal but not zeroCThe currents in the two discharging circuits at t=0 are unequalDC1 loses 50% of its initial charge sooner than C20 loses 50% of its initial charge.Capacitor C1 of the capacitance 1μF and another capacitor C2 of capacitance 2μF are separately charged fully by a common battery.The two capacitors are then separately allowed to discharge through equal resistors at time t=0.
AAt t = 0 the value of current in the circuit containing 1μF is more than current in the circuit containing 2μFBAt t = 0 the current in 2μF capacitor circuit is more than current in 1μF capacitor circuitC1μF capacitor losses 50 % charge sooner than 2μF capacitorD2μF capacitor losses 50 % charge sooner than 1μF capacitorCapacitor C1 of the capacitance 1μF and another capacitor C2 of capacitance 2μF are separately charged fully by a common battery.The two capacitors are then separately allowed to discharge through equal resistors at time t=0.
AThe current in each of the two discharging circuits is zero at t=0BThe current in the two discharging circuits at t=0 are equal but not zeroCThe currents in the two discharging circuits at t=0 are unequalDCapacitor C1 loses 50% of its initial charge sooner than C2 loses 50% of its initial charge
Two capacitors C1andC2(C1>C2) are charged separtately to same potential. Now they are allowed to discharge through similar resistors. Initial rate of discharging will be
View SolutionCapacitor C1 of capacitance 1 micro-farad and capacitor C2 of capacitance 2 microfarad are separately charged fully by a common battery. The two capacitors are then separately allowed to discharged through equal resistors at time t = 0.
View SolutionA charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
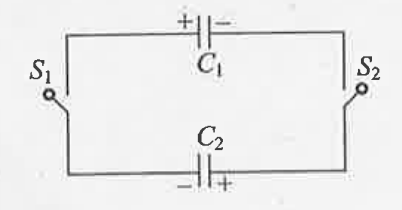
View SolutionTwo capacitors C1andC2 are charged to the same potential V, but with opposite polarity as shown in the figure. The switch S1andS2 are then closed.
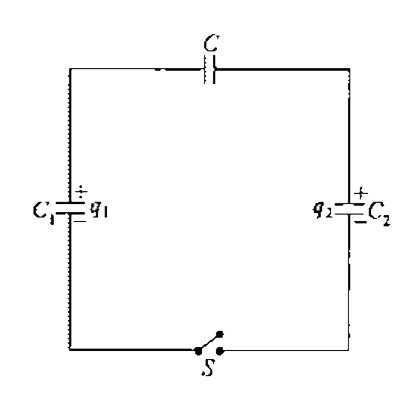
View SolutionTwo capacitor C1 and C2, charged with chargesq1 and q2 then these are connected in series with an uncharged capacitor C, as shown in figure. As the switch S is closed :
View Solution

