A uniform wire of length l and radius r has a resistance of 100Ω. It is recast into wire of radius R2
1600Ω
400Ω
200Ω
100Ω
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Understand the initial conditions
We have a uniform wire of length L and radius R with a resistance of 100Ω.
Step 2: Calculate the volume of the original wire
The volume V of the original wire can be calculated using the formula for the volume of a cylinder:
V=Cross-sectional Area×Length=πR2L
Step 3: Determine the new dimensions after recasting
The wire is recast into a new wire with a radius of R2. Let the new length of the wire be L′. The volume of the new wire is:
V′=π(R2)2L′=πR24L′
Step 4: Set the volumes equal
Since the wire is recast, the volume remains constant:
πR2L=πR24L′
Cancelling πR2 from both sides gives:
L=L′4
Thus, we can express L′ in terms of L:
L′=4L
Step 5: Calculate the new resistance
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
For the original wire:
R=ρLπR2=100Ω
For the new wire:
R′=ρL′A′
where A′=π(R2)2=πR24.
Substituting L′=4L into the resistance formula for the new wire:
R′=ρ(4L)πR24=16ρLπR2
Step 6: Relate new resistance to original resistance
We know from the original resistance:
R=ρLπR2=100Ω
Thus,
R′=16×R=16×100=1600Ω
Final Answer
The new resistance R′ of the wire after recasting is:
1600Ω
We have a uniform wire of length L and radius R with a resistance of 100Ω.
The volume V of the original wire can be calculated using the formula for the volume of a cylinder:
V=Cross-sectional Area×Length=πR2L
The wire is recast into a new wire with a radius of R2. Let the new length of the wire be L′. The volume of the new wire is:
V′=π(R2)2L′=πR24L′
Since the wire is recast, the volume remains constant:
πR2L=πR24L′
Cancelling πR2 from both sides gives:
L=L′4
Thus, we can express L′ in terms of L:
L′=4L
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
R=ρLπR2=100Ω
R′=ρL′A′
where A′=π(R2)2=πR24.
R′=ρ(4L)πR24=16ρLπR2
We know from the original resistance:
R=ρLπR2=100Ω
Thus,
R′=16×R=16×100=1600Ω
The new resistance R′ of the wire after recasting is:
1600Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (ADVANCED) FOR IIT ENTRANCE)
Explore 9 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS WITH MORE THAN ONE CORRECT ANSWER)
Explore 18 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
Explore 20 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A uniform wire of length 1 and radius r has resistance 100Ω. it is recast into a thin wire of (i) length 2l (ii) radius r/2. Calculate the resistance of new wire in each case.
View SolutionA given piece of wire of length l and radius r and resistance R is stretched uniformly to wire of radius r2 .Its new resistance is:
View Solution
Knowledge Check
A uniform wire of length / and radius r has a resistance of 100 Ω. It is recast into a wire of radius r2. The resistance of new wire will be:
A1600ΩB400ΩC200ΩD100ΩA wire of length 5m and radius 1mm has a resistance of 1 ohm . What length of the wire of the same material at the same temperature and of radius 2mm will also have a resistance of 1 ohm
A1.25mB2.5mC10mD20m
A wire of length 1 m and radius 0.1mm gas a resistance of 100(Ω).Find the resistivity of the material .
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and of of 40cm of the potentiometer wire. What is the value of R?
View SolutionA nicrome wire of length 100cm and radius 0.36 mm has a resistance of 1.5Ω. Calculate the resistivity of nicrome and also its conductivity.
View SolutionA potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
View SolutionThe potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
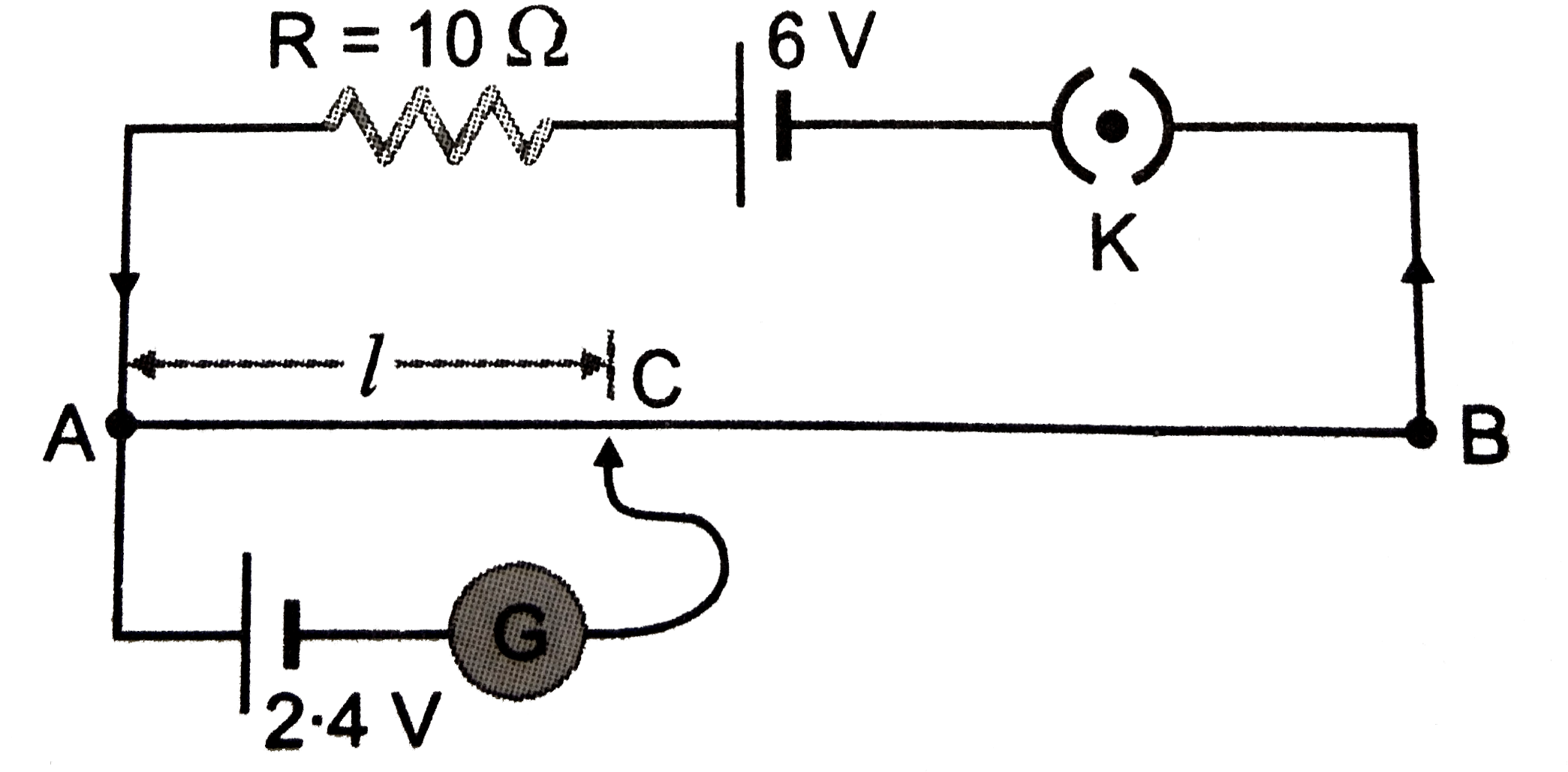
View SolutionA cylindrical wire of length L and radius r has a resistance R. The resistance of another wire of the same material but half its length and half its radius will be:
View Solution

