Three cells of emf, $ε_{1} = 1.5 V, ε_{2} = 2.0 V and ε_{3} = 3.0 V$ having internal resistance $r_{1} = 0.30 Ω, r_{2} = 0.4 Ω and r_{3} = 0.6 Ω$ respectively are connected in parallel. Find out the equivalent emf and the equivalent resistance of a cell which can replace this combination.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of finding the equivalent emf and the equivalent resistance of three cells connected in parallel, we will follow these steps:
Step 1: Write down the given values
We have three cells with the following parameters:
- Cell 1: $ϵ_{1} = 1.5 V$ , $r_{1} = 0.30 Ω$
- Cell 2: $ϵ_{2} = 2.0 V$ , $r_{2} = 0.40 Ω$
- Cell 3: $ϵ_{3} = 3.0 V$ , $r_{3} = 0.60 Ω$
Step 2: Calculate the equivalent emf ( $ϵ_{n e t}$ )
The formula for the equivalent emf of cells in parallel is given by:
$ϵ_{n e t} = \frac{ϵ_{1} / r_{1} + ϵ_{2} / r_{2} + ϵ_{3} / r_{3}}{1 / r_{1} + 1 / r_{2} + 1 / r_{3}}$
Substituting the values:
$ϵ_{n e t} = \frac{(1.5 / 0.30) + (2.0 / 0.40) + (3.0 / 0.60)}{(1 / 0.30) + (1 / 0.40) + (1 / 0.60)}$
Calculating the numerator:
$\frac{1.5}{0.30} = 5, \frac{2.0}{0.40} = 5, \frac{3.0}{0.60} = 5$
$Numerator = 5 + 5 + 5 = 15$
Calculating the denominator:
$\frac{1}{0.30} = \frac{10}{3}, \frac{1}{0.40} = \frac{5}{2}, \frac{1}{0.60} = \frac{5}{3}$
Finding a common denominator (which is 6):
$\frac{10}{3} = \frac{20}{6}, \frac{5}{2} = \frac{15}{6}, \frac{5}{3} = \frac{10}{6}$
$Denominator = \frac{20 + 15 + 10}{6} = \frac{45}{6}$
Now substituting back into the formula:
$ϵ_{n e t} = \frac{15}{\frac{45}{6}} = 15 \times \frac{6}{45} = 2 V$
Step 3: Calculate the equivalent resistance ( $R_{e q}$ )
The equivalent resistance for resistors in parallel is calculated using:
$\frac{1}{R_{e q}} = \frac{1}{r_{1}} + \frac{1}{r_{2}} + \frac{1}{r_{3}}$
Substituting the values:
$\frac{1}{R_{e q}} = \frac{1}{0.30} + \frac{1}{0.40} + \frac{1}{0.60}$
Calculating each term:
$\frac{1}{0.30} = \frac{10}{3}, \frac{1}{0.40} = \frac{5}{2}, \frac{1}{0.60} = \frac{5}{3}$
Finding a common denominator (which is 6):
$\frac{10}{3} = \frac{20}{6}, \frac{5}{2} = \frac{15}{6}, \frac{5}{3} = \frac{10}{6}$
$\frac{1}{R_{e q}} = \frac{20 + 15 + 10}{6} = \frac{45}{6}$
Thus,
$R_{e q} = \frac{6}{45} = \frac{2}{15} Ω$
Final Results
- Equivalent emf ( $ϵ_{n e t}$ ) = 2 V
- Equivalent resistance ( $R_{e q}$ ) = $\frac{2}{15} Ω$

Updated on:18/9/2024

Two resistor of resistance $R_{1} = (6 \pm 0.09) Ω$ and $R_{2} = (3 \pm 0.09) Ω$ are connected in parallel the equivalent resistance R with error (in $Ω)$
A $R = (2 \pm 0.04)$
B $R = (2 \pm 0.05)$
C $R = (9 \pm 0.18)$
D $R = (2 \pm 0.18)$
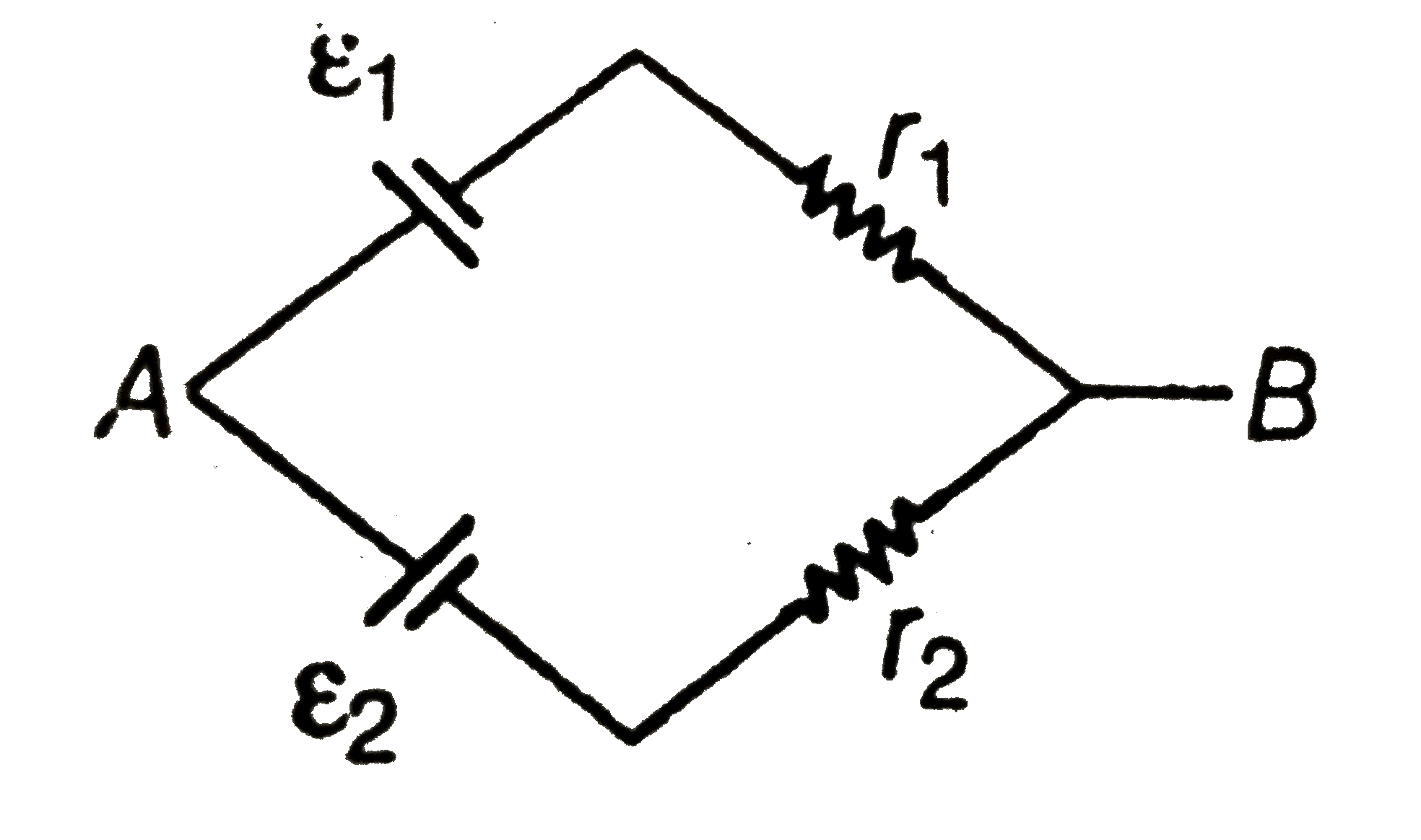
Two batteries of emf $ε_{1} and ε_{2} (ε_{2} > ε_{1})$ and internal resistance $r_{1} and r_{2}$ respectively are connected in parallel as shown in figure.
AThe equivalent emf $ε_{e q}$ of the two cells is between $ε_{1} and ε_{2}$ , i.e., $ε_{1} < ε_{e q} < ε_{2}$
Bthe equivalent emf $ε_{e q}$ is smaller than $ε_{1}$
CThe $ε_{e q}$ is given by $ε_{e q} = ε_{1} + ε_{2}$ always.
D $ε_{e q}$ is independent of internal resistance $r_{1} and r_{2}$ .