(a) State the principle of a potentiometer. Define potential gradient. Obtain an expression for potential gradient in terms of resistivity of the potentiometer wire.
(b) The figure shows a long potentiometer wire AB having a constant potential gradient. The null points for the two primary cells of emf ε1andε2 connected in the manner shown are obtained at a distance of l1=120cmandl2=300cm from th end A. Determine (i) ε1/ε2 and (ii) position of null point for the cell ε1 only.

(b) Using formula
ε1−ε2ε1+ε2=120300=25
Using componendo and dividendo,
⇒ε1ε2=73
⇒E.=ε1−ε2=ε1−37ε1⇒E.=4ε17
∴ Balanced point for E.. is obtained at l1=120cm
⇒ Balanced point for 4ε17 is obtained at, l1=120cm
⇒ Balanced point for ε1 is obtained at l1=7×1204=7×30=210cm
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:REVISION EXERCISES (NUMERICAL PROBLEMS)
Explore 24 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (A. MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER)
Explore 36 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:REVISION EXERCISES (SHORT ANSWER QUESTIONS)
Explore 37 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
In the Fig., a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emf ε1 and ε2 connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i)ε1/ε2 and (ii) position of null point for the cell ε1. How is the sensitivity of a potentiometer increased ?

View SolutionIn the figure a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emfs ε1 and ε2 connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i) ε1/ε2 and (ii) position of null point for the cell ε1.
How is the sensitivity of a potentiometer increased ?
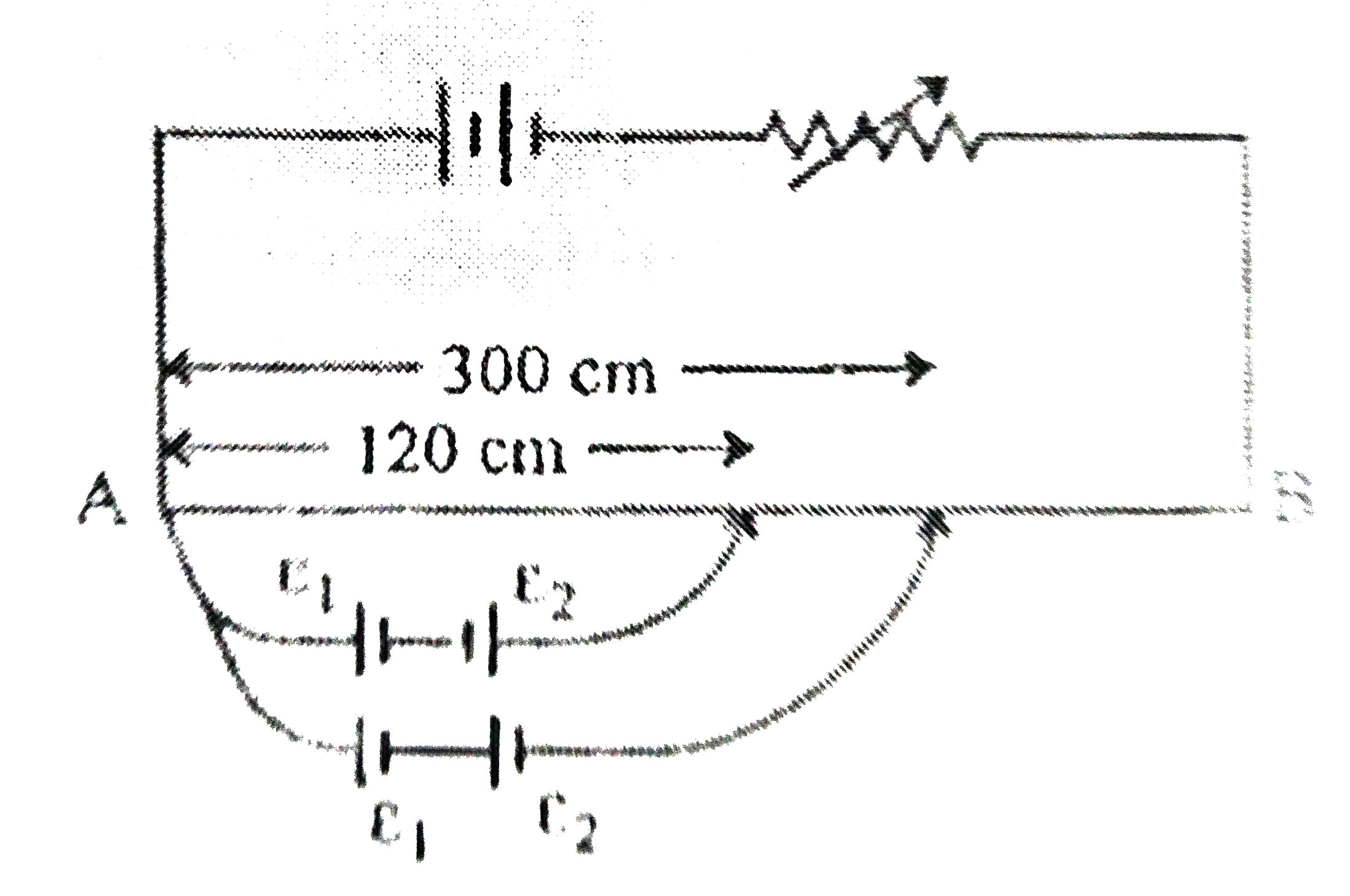
View Solution
Knowledge Check
In potentiometer the potential gradient is –
Aresistance across the unit length of the wireBcurrent across the unit length of the wireCpotential difference across the unit length of the wireDpower across the unit length of the wireIf the resistivity of a potentiometer wire be ρ and area of cross-section be A , then what will be potential gradient along the wire
AIρABIAρCIAρDIAρAs is the cross sectional area and ρ is the specific resistance of a potentiometer wire. If I is the current passing through the potentiometer wire, then the potential gradient along the length of the wire is given by
AIAρBIAρCIρADIρA
In the figure a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emfs ε1 and ε2 connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i) ε1/ε2 and (ii) position of null point for the cell ε1.
How is the sensitivity of a potentiometer increased ?
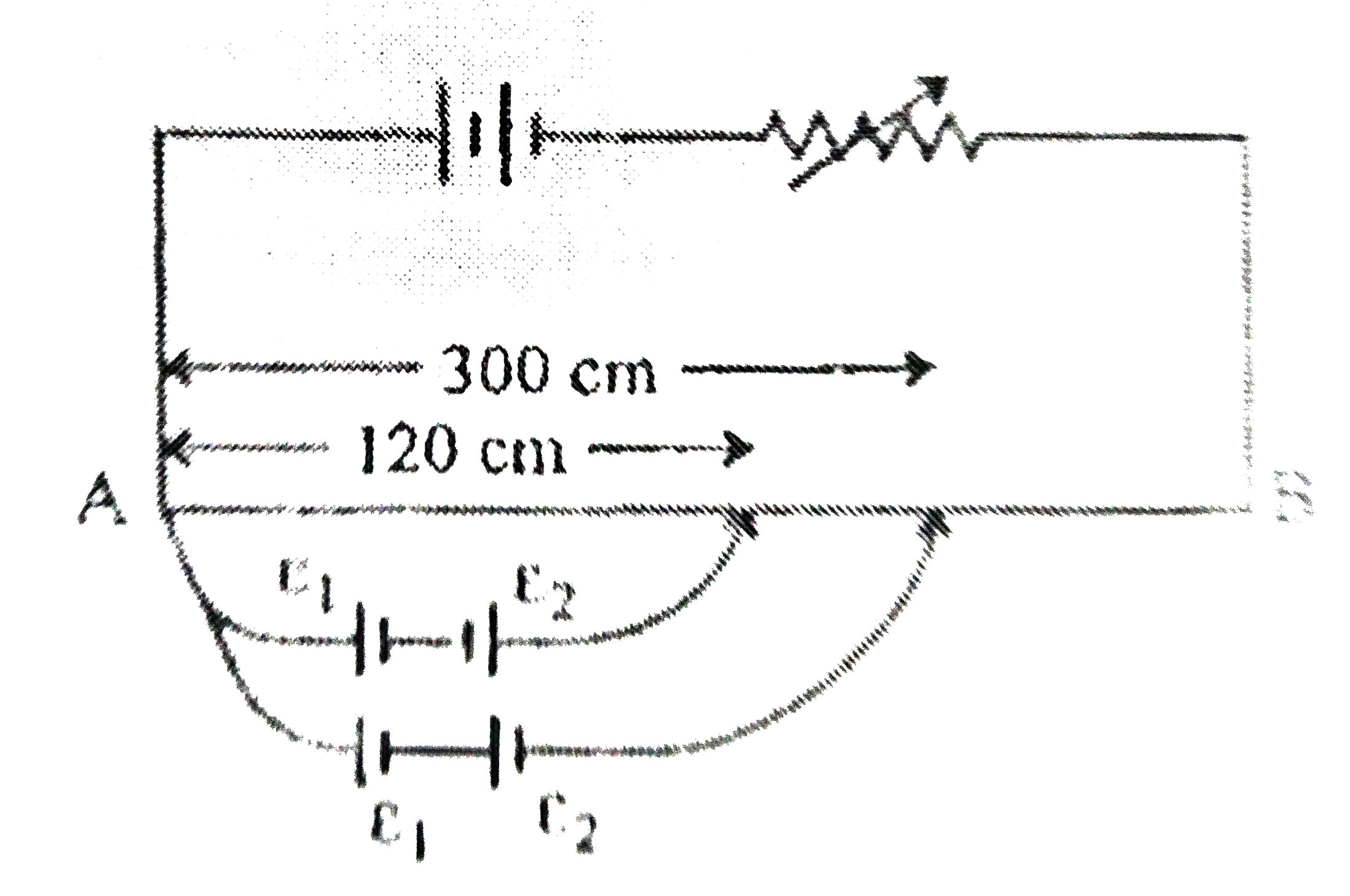
View SolutionIf the resistivity of a potentiometer wire be ρ and area of cross-section be A , then what will be potential gradient along the wire
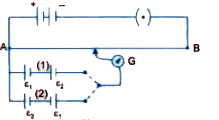
View SolutionA circuit using a potentiometer and battery of negligible internal resistance is set up as shown in Fig. to develop a constant potential gradient along the wire AB. Two cells of emfs ε1 and ε2 are connected in series as shown in combinations (1) and (2). The balance points are obtained respectively at 400 cm and 240 cm from the point A. Find (i) ε1ε2 , (ii) balancing length for the cell ε1 only .
View SolutionThe potential gradient for a potentiometer depends on
View SolutionThe potential gradient for a potentiometer depends on
View Solution

