The relaxation time τ is nearly independent of applied electric field E whereas it changes significiantly with temperature T. First fact is (in part) responsible for Ohm's law whereas the second fact leads to variation of p with temperature. Elaborate why ?
The relaxation time depends on the velocities of electrons and ions. The applied electric field brings a very insignificant change in the velocities of electrons. This is turn keep ρ constant and Ohm.s law is follwed. On the other hand, on varying the temperature, the velocities of electrons and ions are changed very significantly. Thus, the relaxation time is altered to a large extent, which in turn changes the resistivity significantly. This leads to variation of ρ with temperature.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:NCERT SOLVED (NCERT Exemplar Problems Subjective Questions)(Short Answers Type Questions)
Explore 6 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
Explore 10 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:NCERT SOLVED (NCERT Additional Exercises)
Explore 11 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Dependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
The enthalpy change for a certain rection at 300 K is −15.0 K cal mol−1 . The entropy change under these conditions is −7.2 cal K−1mol−1 . The free energy change for the reaction and its spontaneous/ non-spontaneous character will be
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 298K,2A+B→C
ΔH=100kcal and ΔS=0.050kcalK−1. If ΔH and ΔS are assumed to be constant over the temperature range, above what temperature will the reaction become spontaneous?
View Solution
Knowledge Check
Dependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
When CaCO3 is heated to a high temperature , it undergoes decomposition into CaO and CO2 whereas it is quite stable at room temperature . The most likely explanation of it, isAThe enthalpy of reaction (ΔH) overweighs the term TΔS at high temperature.BThe term TΔS overweighs the enthalpy of reaction at high temperature.CAt high temperature , both enthalpy of reaction and entropy change become negative.DNone of theseFor a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
When CaCO3 is heated to a high temperature, it undergoes decomposition into CaO and CO2 whereas it is quite stable at room temperature. The most likely explanation of it, is:Athe enthalpy of reaction (ΔH) outweighs the term TΔS at high temperatureBthe term TΔS outweighs the enthalpy of reaction at high temperatureCat high temperature, both enthalpy of reaction and entropy change become negativeDnone of the aboveElectrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value of zero as their temperature is lowered below a critical temperature TC(0). An interesting property of super conductors is that their critical temperature becomes smaller than TC(0) if they are placed in a magnetic field, i.e., the critical temperature TC(B) is a function of the magnetic field strength B. The dependence of TC(B) on B is shown in the figure.
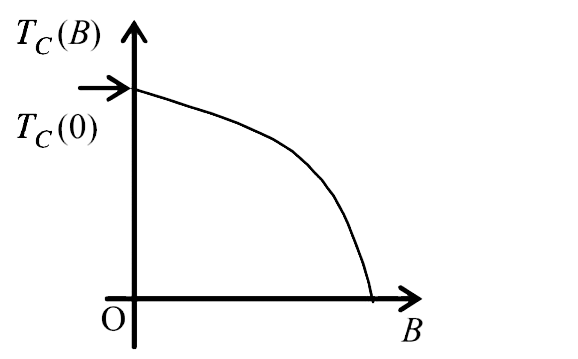 .
.
In the graphs below, the resistance R of a superconductor is shown as a function of its temperature T for two different magnetic fields B1(solid line) and B2 (dashed line). If B2 is larget than B1 which of the following graphs shows the correct variation of R with T in these fields?A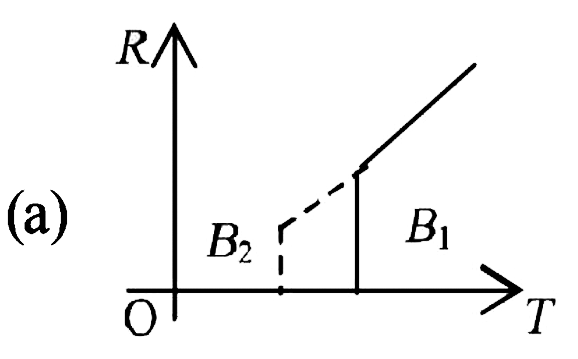 B
B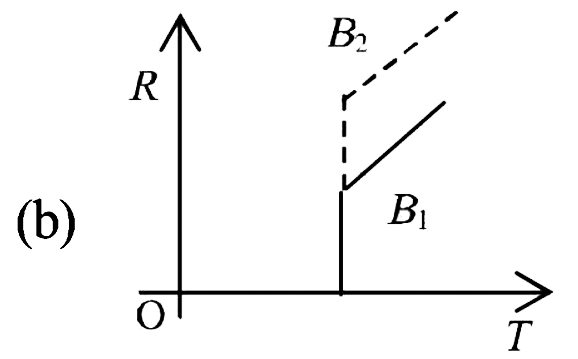 C
C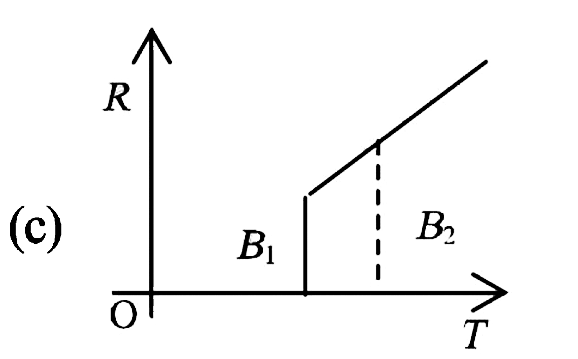 D
D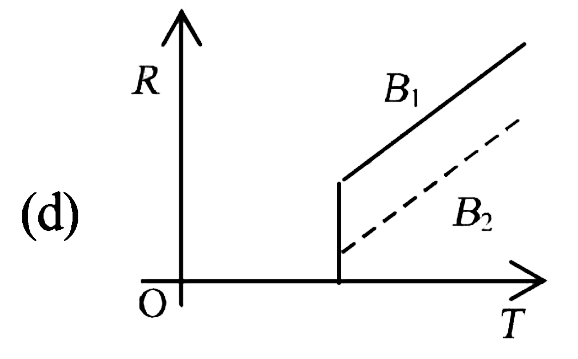
Dependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
A reaction has a value of ΔH=−40Kcal at 400 k cal mol−1. The reaction is spontaneous, below this temperature , it is not . The values fo ΔG and ΔS at 400 k are respectively
View SolutionFor a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
The enthalpy change for a certain reaction at 300K is -15.0 k cal mol−1 . The entropy change under these conditions is -7.2 cal K−1mol−1. The free energy change for the reaction and its spontaneous/non-spontaneous character will be :
View SolutionFor a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 298K, 2A+B→C ΔH=100 kcal and ΔS=0.050 kcal K−1. If ΔH and ΔS are assumed to be constant over the temperature range, just above what temperature will be reaction become spontaneous?
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 25∘,X2O4(l)→2XO2(g)
ΔH=2.1Kcal and ΔS=20calK−1. The reaction would be
View SolutionFor a process top be spontaneous, at constant temperature and pressure, there must be decreases in free energy of the system in the direction of the process, i.e. ΔGP.T.<0.ΔP.T.=0 implies the equilibrium condition and ΔGP.T.>0 corresponding to non-spontaneity.
Gibb's Helmholtz equation relates the free energy change to the enthalpy and entropy change of the process as :
ΔGP.T.=ΔH−TΔS......(i)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For edothermic proces, both ΔHand ΔS are positive. The energy factor,the first factor of equation, opposes the spontaneity whereas entropy factor favours it . At low temperature, the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicating the non-spontaneity of the process. On raising temperature, the factor TΔS increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous.
For an exothermic process, both ΔH and ΔS would be negative. In this case, the first factor of equation(i) favours the spontaneity whereas the second factor opposes it. At high temperature, when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity of the process. However, on decreasing temperature, the factore TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus, an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
A reaction has a value of ΔH=-40 kcal at 400K . Above 400K, the reaction is spontaneous, below this temperature, it is not. The value of ΔG and ΔS at 400K are respectively:
View Solution

