A constant voltage of 3 V is supplied to a potentiometer wire. A cell of emf 2 V is balanced by a voltage drop across 416 cm of the wire. Find the total length of the potentiometer wire.
To solve the problem, we need to find the total length of the potentiometer wire (L) using the information given about the voltage supplied and the voltage drop across a certain length of the wire.
1. Identify the Given Values:
- Voltage supplied to the potentiometer wire (V) = 3 V
- EMF of the cell (E) = 2 V
- Length of wire balanced by the cell (d) = 416 cm
2. Understand the Concept of Potential Gradient:
- The potential gradient (k) of the potentiometer wire is defined as the voltage per unit length of the wire. It can be expressed as:
k=VL
- Where V is the voltage across the entire length of the wire (3 V) and L is the total length of the wire.
3. Set Up the Equation for the Known Length:
- For the length of the wire that balances the cell (416 cm), the potential gradient can also be expressed as:
k=Ed
- Where E is the EMF of the cell (2 V) and d is the length of wire (416 cm).
4. Equate the Two Expressions for Potential Gradient:
- Since the potential gradient is constant along the wire, we can set the two expressions equal to each other:
VL=Ed
- Substituting the known values:
3L=2416
5. Cross Multiply to Solve for L:
- Cross multiplying gives us:
3⋅416=2⋅L
- Simplifying this:
1248=2L
6. Solve for L:
- Dividing both sides by 2:
L=12482=624 cm
Final Answer:
The total length of the potentiometer wire is 624 cm.
- Voltage supplied to the potentiometer wire (V) = 3 V
- EMF of the cell (E) = 2 V
- Length of wire balanced by the cell (d) = 416 cm
- The potential gradient (k) of the potentiometer wire is defined as the voltage per unit length of the wire. It can be expressed as:
k=VL
- Where V is the voltage across the entire length of the wire (3 V) and L is the total length of the wire.
- For the length of the wire that balances the cell (416 cm), the potential gradient can also be expressed as:
k=Ed
- Where E is the EMF of the cell (2 V) and d is the length of wire (416 cm).
- Since the potential gradient is constant along the wire, we can set the two expressions equal to each other:
VL=Ed
- Substituting the known values:
3L=2416
- Cross multiplying gives us:
3⋅416=2⋅L
- Simplifying this:
1248=2L
- Dividing both sides by 2:
L=12482=624 cm
The total length of the potentiometer wire is 624 cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS
Explore 71 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:CONCEPTUAL QUESTIONS
Explore 35 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Figure shows a potentiometer circuit, a cell of emf E1 is balanced by length l' of the potentiometer wire. If this cell is replaced by another of emf E2, it is found that total length of potentiometer wire has to be increased by 50%, in order to have the same balance length (l'). Then E1/E2 is______.

View SolutionA potentiometer wire has resistance of per unit length of 0.1Ω/m. A cell of e.m.f. 1.5V balances against 300cm length of the wire. Find the current in the potentiometer wire.
View Solution
Knowledge Check
A steady voltage drop is maintained across a potentiometer wire which is 5m long. A Daniel cell is balanced by a length of 3m of wire. If length of potentiometer wire is increased to 6 m, find new length of wire across which Daniel cell will be balanced.
A3.6mB6.6mC6.3 mD3.3mIn an experiment to find the internal resistance of a cell by a potentiometer, a balance was obtained for 50 cm length of the potentiometer wire, with a cell of e.m.f. 2V. When the cell was shunted by a resistance of 2Ω, the balancing length of the potentiometer wire was 40 cm. What was the internal resistance of the cell ?
A0.25ΩB0.75ΩC0.5ΩD1ΩA potentiometer wire is 10 m long and a P.D. of 6 V is maintained between its ends. The e.m.f. of the cell which balances against a length of 200 cm of the potentiometer wire is
A1 VB1.2 VC2.4 VD1.5V
The potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
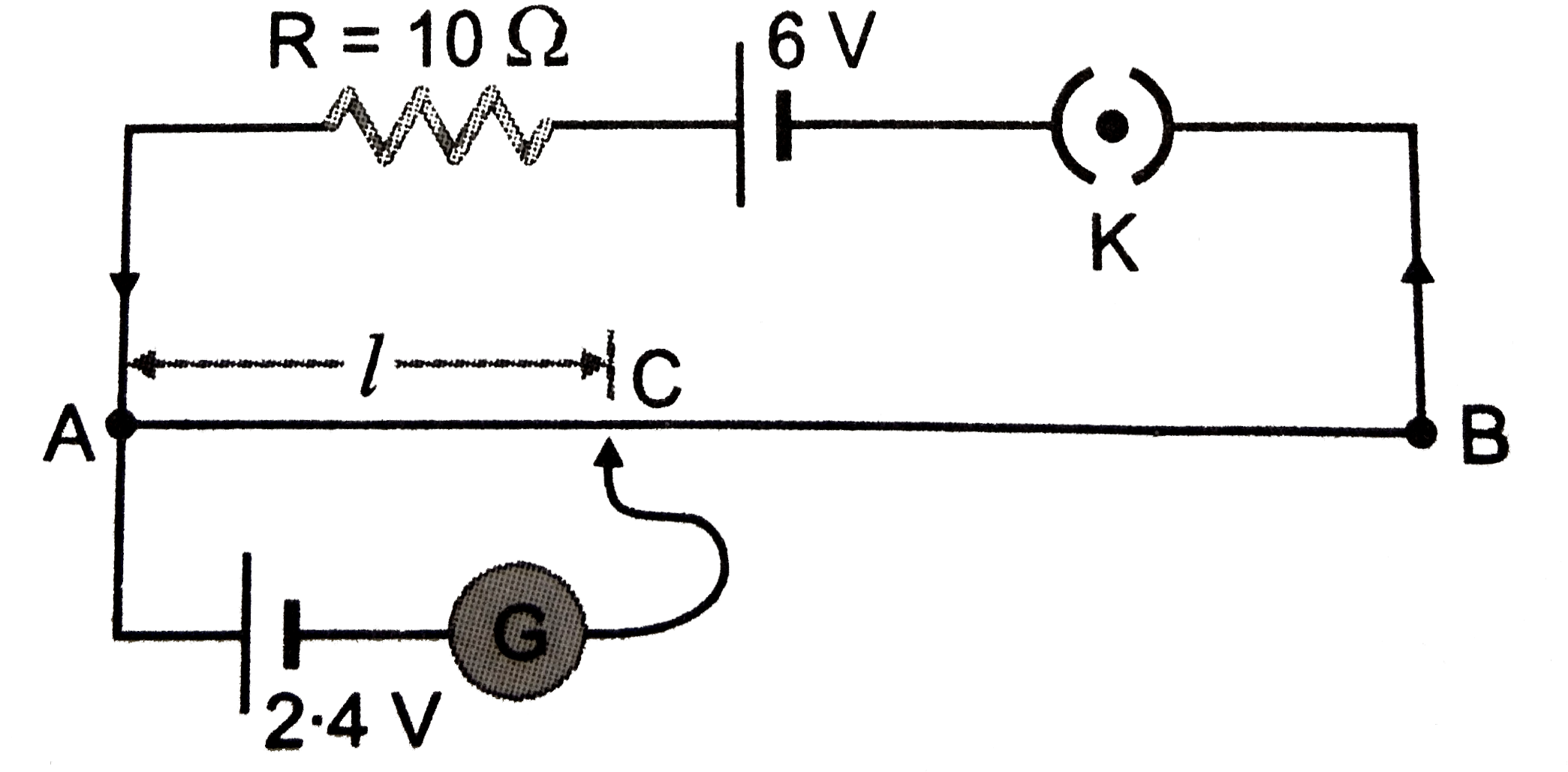
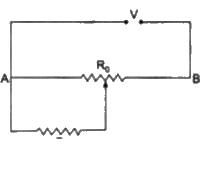
View SolutionA resistance of R draw current from a potentiometer. The potentiometer wire, AB, has total resistance of R0. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire.
View SolutionA 10 wire potentiometer has first five wires of cross sectional radius r and next five wires of radius 2r. The wires are uniform and made of same material. An ideal cell of emf 2V is connected across the potentiometer wire. What length of the potentiometer wire will balance the emf of–
(a) a Daniell cell (emf = 1.0 V)
(b) a Lechlanche cell (emf = 1.5 V)
(c) a cell of emf 1.8 V ?
Length of each wire is 100 cm.
View SolutionThe balancing length for a cell in a potentiometer experiment is 45 cm. In the balanced condition, the current through the potentiometer wire is 2 A. If the total length of the potentiometer wire is 1 m and its total resistance is60Ω , the emf of the cell is (in Volts) _________.
View SolutionThe length of a potentiometer wire is l. A cell of emf E is balanced at a length l/3 from the positive end of the wire. If the length of the wire is increased by l/2. At what distance will the same cell give a balance point.
View Solution

