A resistance of 97Ω is connected to a battery of emf 10 V . To measure the current passing in the circuit, an ammeter is inserted in series with the resistance. It is found that the ammeter reads 100 mA. What is the internal resistance of the battery if 2Ω is the resistance of ammeter ?
To find the internal resistance of the battery, we can follow these steps:
Step 1: Identify the known values
- Resistance of the external resistor, R=97Ω
- EMF of the battery, E=10V
- Current measured by the ammeter, I=100mA=0.1A
- Resistance of the ammeter, ra=2Ω
Step 2: Calculate the total resistance in the circuit
The total resistance Rtotal in the circuit is the sum of the external resistance, the internal resistance of the battery r, and the resistance of the ammeter:
Rtotal=R+ra+r
Substituting the known values:
Rtotal=97Ω+2Ω+r=99Ω+r
Step 3: Use Ohm's Law to relate voltage, current, and resistance
According to Ohm's Law:
V=I×Rtotal
Here, the voltage V is equal to the EMF of the battery E:
10V=0.1A×(99Ω+r)
Step 4: Rearrange the equation to solve for r
Now, we can rearrange the equation:
10=0.1×(99+r)
Dividing both sides by 0.1:
100=99+r
Now, isolate r:
r=100−99=1Ω
Step 5: Conclusion
The internal resistance of the battery is:
r=1Ω
---
- Resistance of the external resistor, R=97Ω
- EMF of the battery, E=10V
- Current measured by the ammeter, I=100mA=0.1A
- Resistance of the ammeter, ra=2Ω
The total resistance Rtotal in the circuit is the sum of the external resistance, the internal resistance of the battery r, and the resistance of the ammeter:
Rtotal=R+ra+r
Substituting the known values:
Rtotal=97Ω+2Ω+r=99Ω+r
According to Ohm's Law:
V=I×Rtotal
Here, the voltage V is equal to the EMF of the battery E:
10V=0.1A×(99Ω+r)
Now, we can rearrange the equation:
10=0.1×(99+r)
Dividing both sides by 0.1:
100=99+r
Now, isolate r:
r=100−99=1Ω
The internal resistance of the battery is:
r=1Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS
Explore 71 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:CONCEPTUAL QUESTIONS
Explore 35 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionA resistance of 1Ω is connected to a battery of emf 2 V and internal resistance 0.4Ω what current is flowing through the circuit ? If another battery of double the emf is connected in series with the earlier one then current flowing in the circuit becomes double . what should be the internal resistance of battery ?
View Solution
Knowledge Check
In the above question, if the internal resistance of the battery is 1 ohm , then what is the reading of ammeter
A5/3AB40/29AC10/9AD1AIn an ammeter, 4% of the total current is passing through the galvanomter. If the shunt resistance is 5Ω, then the resistance is Omega, then the resistance of the galvanometer will be
A30ΩB60ΩC120ΩD240Ω
An ammeter of resistance 1 W can measure current upto 1.0 A. (i) What must be the value of the shunt resistance to enable the ammeter to measure upto 5.0 A? (ii) What is the combined resistance of the ammeter and the shunt?
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA battery of emf 3V and internal resistance r is connected in series with a resistor of 55Ω through an ammeter of resistance 1Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA battery of emf 3 volt and internal resistance r is connected in series with a resistor of 55Ω through an ammeter of resistance 1Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View Solution(a) A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance 100Ω. When a voltmeter is connected across the 100Ω resistance the ammeter reading is 0.04A. Find the voltage read by the voltmeter and its resistance. Had the voltmeter been an ideal one, what would have its reading ?
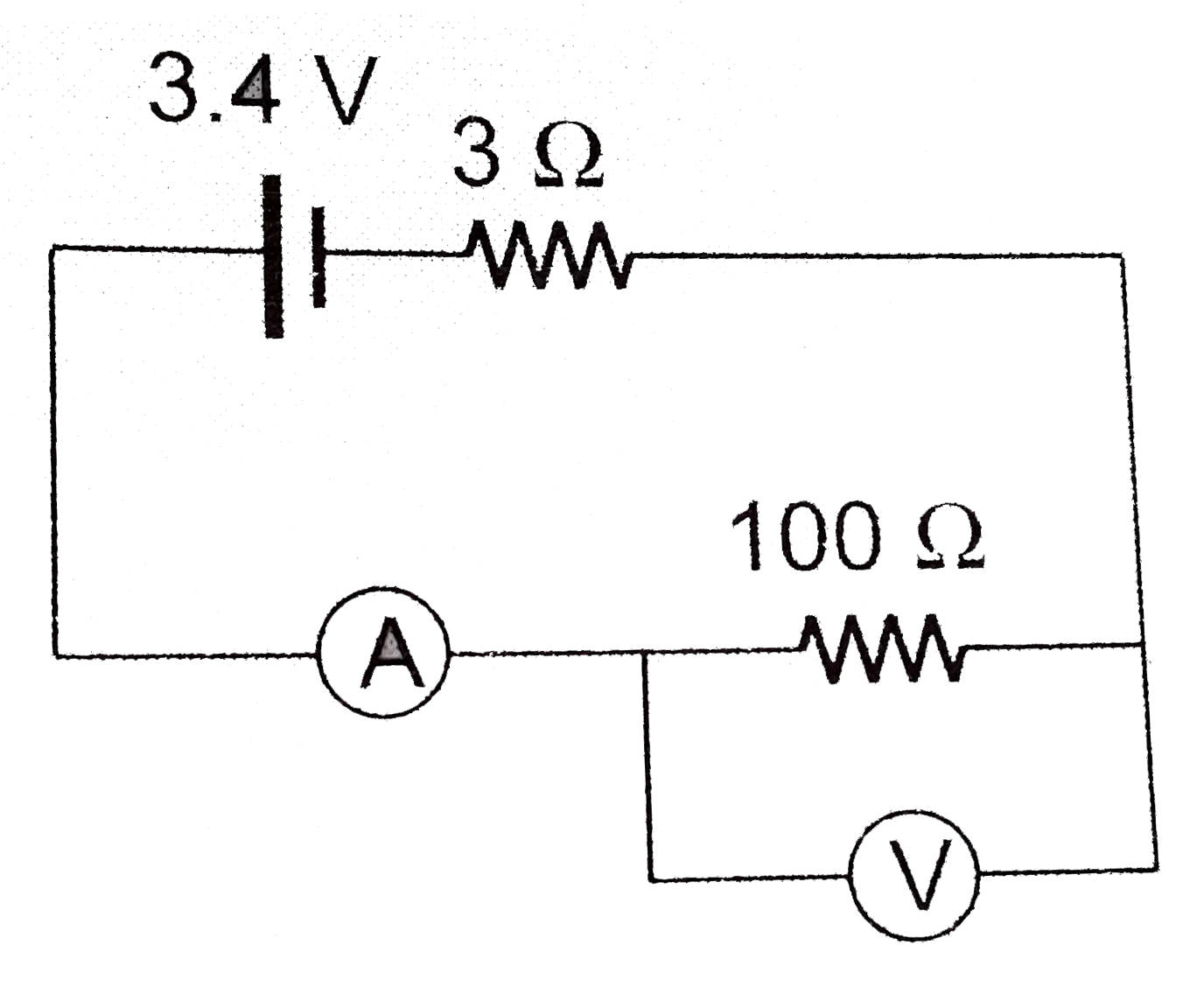
(b) Two resistances of 100Ω and 200Ω are connected in series with battery of emf 4V and negligible internal resistance. A voltmeter of resistance 200Ω is used to measure voltemeter of resistances separately. Calculate the voltmeter indicated.
( c) In the circuit shown, a voltmeter reads 30V when it is connected across the 400Ω resistance. Calculate what the same voltmeter will read when it is connected across the 300Ω resistance ?
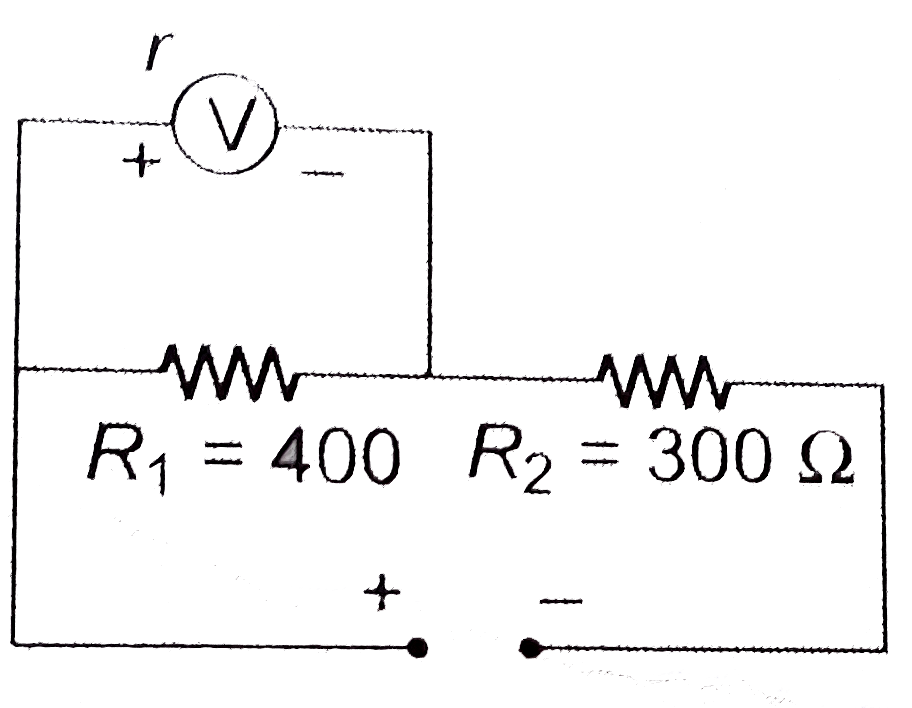
(d) An ammeter and a voltmeter are connected in series to a battery of emf E=6.0V. When a certain resistance is connected in parallel with the voltmeter. the reading of the ammeter is doubled. while voltmeter reading is reduced to half. Find the voltmeter reading after the connection of the resistance.
View Solution

