Two cylinders P and Q of equal mass are made from the same metal. If the radius of P is n times the radius of Q , then calculate ratio of their resistances.
To solve the problem of finding the ratio of the resistances of two cylinders P and Q made from the same metal and having equal mass, we can follow these steps:
Step 1: Understand the relationship between mass, volume, and density
Since both cylinders are made from the same metal, they have the same density (ρ). The mass (m) of each cylinder can be expressed in terms of its volume (V) and density:
m=ρV
Thus, for both cylinders:
VP=VQ
Step 2: Express the volume of the cylinders
The volume (V) of a cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height (or length) of the cylinder. For cylinders P and Q, we can write:
VP=πr2PlP
VQ=πr2QlQ
Step 3: Set the volumes equal to each other
Since the masses are equal, we have:
πr2PlP=πr2QlQ
Cancelling π from both sides gives:
r2PlP=r2QlQ
Step 4: Relate the radii of the cylinders
Given that the radius of P is n times the radius of Q:
rP=nrQ
Substituting this into the volume equation gives:
(nrQ)2lP=r2QlQ
This simplifies to:
n2r2QlP=r2QlQ
Dividing both sides by r2Q (assuming rQ≠0):
n2lP=lQ
Thus, we can express the lengths in terms of each other:
lP=lQn2
Step 5: Calculate the resistances of the cylinders
The resistance R of a cylinder is given by:
R=ρlA
where A is the cross-sectional area. The area A for a cylinder is:
A=πr2
Thus, the resistances for cylinders P and Q can be expressed as:
RP=ρlPπr2P
RQ=ρlQπr2Q
Step 6: Find the ratio of the resistances
Now, we can find the ratio RPRQ:
RPRQ=ρlPπr2PρlQπr2Q=lPlQ⋅r2Qr2P
Substituting lP=lQn2 and rP=nrQ:
RPRQ=lQn2lQ⋅r2Q(nrQ)2=1n2⋅r2Qn2r2Q=1n2⋅1n2=1n4
Final Ratio of Resistances
Thus, the ratio of the resistances is:
RPRQ=1n4
or equivalently,
RQRP=n4
Since both cylinders are made from the same metal, they have the same density (ρ). The mass (m) of each cylinder can be expressed in terms of its volume (V) and density:
m=ρV
Thus, for both cylinders:
VP=VQ
The volume (V) of a cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height (or length) of the cylinder. For cylinders P and Q, we can write:
VP=πr2PlP
VQ=πr2QlQ
Since the masses are equal, we have:
πr2PlP=πr2QlQ
Cancelling π from both sides gives:
r2PlP=r2QlQ
Given that the radius of P is n times the radius of Q:
rP=nrQ
Substituting this into the volume equation gives:
(nrQ)2lP=r2QlQ
This simplifies to:
n2r2QlP=r2QlQ
Dividing both sides by r2Q (assuming rQ≠0):
n2lP=lQ
Thus, we can express the lengths in terms of each other:
lP=lQn2
The resistance R of a cylinder is given by:
R=ρlA
where A is the cross-sectional area. The area A for a cylinder is:
A=πr2
Thus, the resistances for cylinders P and Q can be expressed as:
RP=ρlPπr2P
RQ=ρlQπr2Q
Now, we can find the ratio RPRQ:
RPRQ=ρlPπr2PρlQπr2Q=lPlQ⋅r2Qr2P
Substituting lP=lQn2 and rP=nrQ:
RPRQ=lQn2lQ⋅r2Q(nrQ)2=1n2⋅r2Qn2r2Q=1n2⋅1n2=1n4
Thus, the ratio of the resistances is:
RPRQ=1n4
or equivalently,
RQRP=n4
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS
Explore 71 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:CONCEPTUAL QUESTIONS
Explore 35 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
There are two wires P and Q made of the same material and both have the same mass . The radius of wire P is half the radius of the wire Q. the resistance of P is 24Ω. Find the resistance of Q.
View SolutionBy melting a solid cylindrical metal,a few conical materials are to be made. If three times the radius of the cone is equal to twice the radius of the cylinder and the ratio of the height of the cylinder and the height of the cone is 4:3, find the number of cones which can be made
View Solution
Knowledge Check
The radius and height of a cylinder are equal. If the radius of the sphere is equal to the height of the cylinder, then the ratio of the rates of increase of the volume of the sphere and the volume of the cylinder, is
A4:3B3:4C4:3πD3π:4The volume of two cylinders are equal and their heights are in the ratio 1:3. Then, the ratio of their radius are
A4:√3B3:2√3C2:√3D3:√3Two circular coils P and Q are made from similar wire but radius of Q is twice that of P. Relation between the values of potential difference across them so that the magnetic induction at their centers may be the same is
AVq=2VpBVq=3VpCVq=4VpDVq=1/4Vp
Spheres P and Q are uniformally constructed from the same material which is good conductor of heat and the radius of Q is thrice the radius of P. The rate of fall of temperature of P is x times that of Q when both are at the same surface temperture. Find the value of 'x' :
View Solution1 meter long metallic wire is broken into two unequal parts PandQP part of the wire in uniformly extended into another wire R. Length of R is twice the length of P and the resistance of R is equal to that of Q. Find the ratio of the resistance P and R and also the ratio of the length PandQ
View SolutionA wire made of material A has resistance R1 another wire made of material B having P time the length and q times the radius of first wire has resistance R2 . If resistivity of B is r times that of A, then calculateR2/R1 .
View SolutionIn the given figure, two wheels P and Q are connected by a belt B. The radius of P is three times as that of Q. In case of same rotational kinetic energy, the ratio of rotational inertias (I1I2) will be x:1 The value of x will be ________
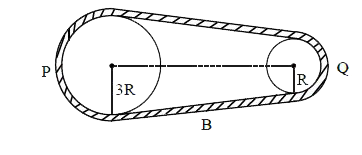
View SolutionA large solid metallic cylinder whose radius and height are equal to each other is to be melted and 48 identical solid balls are to be recast from the liquid metal so formed. What is the ratio of the radius of a ball to the radius of the cylinder?
View Solution

