Radius of a nucleus is given by the relation $R = R_{0} A^{1 / 3}$ where $R_{0} = 1.3 \times 10^{- 15} m$ and A is mass number. For a nucleon inside a nucleus, de-Broglie wavelength is given by diameter of the nucleus. Average kinetic energy of a nucleon in the $T e^{128}$ nucleus based on above information will be :

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $3.09 \times 10^{10} K$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Radius of a nucleus is given by the relation R = R_(0)A^(1//3) where R_(0) = 1.3 xx 10^(-15) m and A is mass number. For a nucleon inside a nucleus, de-Broglie wavelength is given by diameter of the nucleus. Average kinetic energy of a nucleon in the Te^(128) nucleus based on above information will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS NUCLEAR PHYSICS

Topper's Solved these Questions

Knowledge Check

The radius of a nucleus is given by $r_{0} A^{1 / 3}$ where $r_{0} = 1.3 \times 10^{- 15}$ m and A is the mass number of the nucleus, the Lead nucleus has A = 206. the electrostatic force between two protons in this nucleus is approximately
A $10^{2}$ N
B $10^{7}$ N
C $10^{12}$ N
D $10^{17}$ N
If there are N nucleons in a nucleus of radius R, then the number of nucleons in a nucleus of radius 2R will be :
AN
B2N
C8N
D $2^{1 / 3} N$
Read the following passage carefully and answer the questions

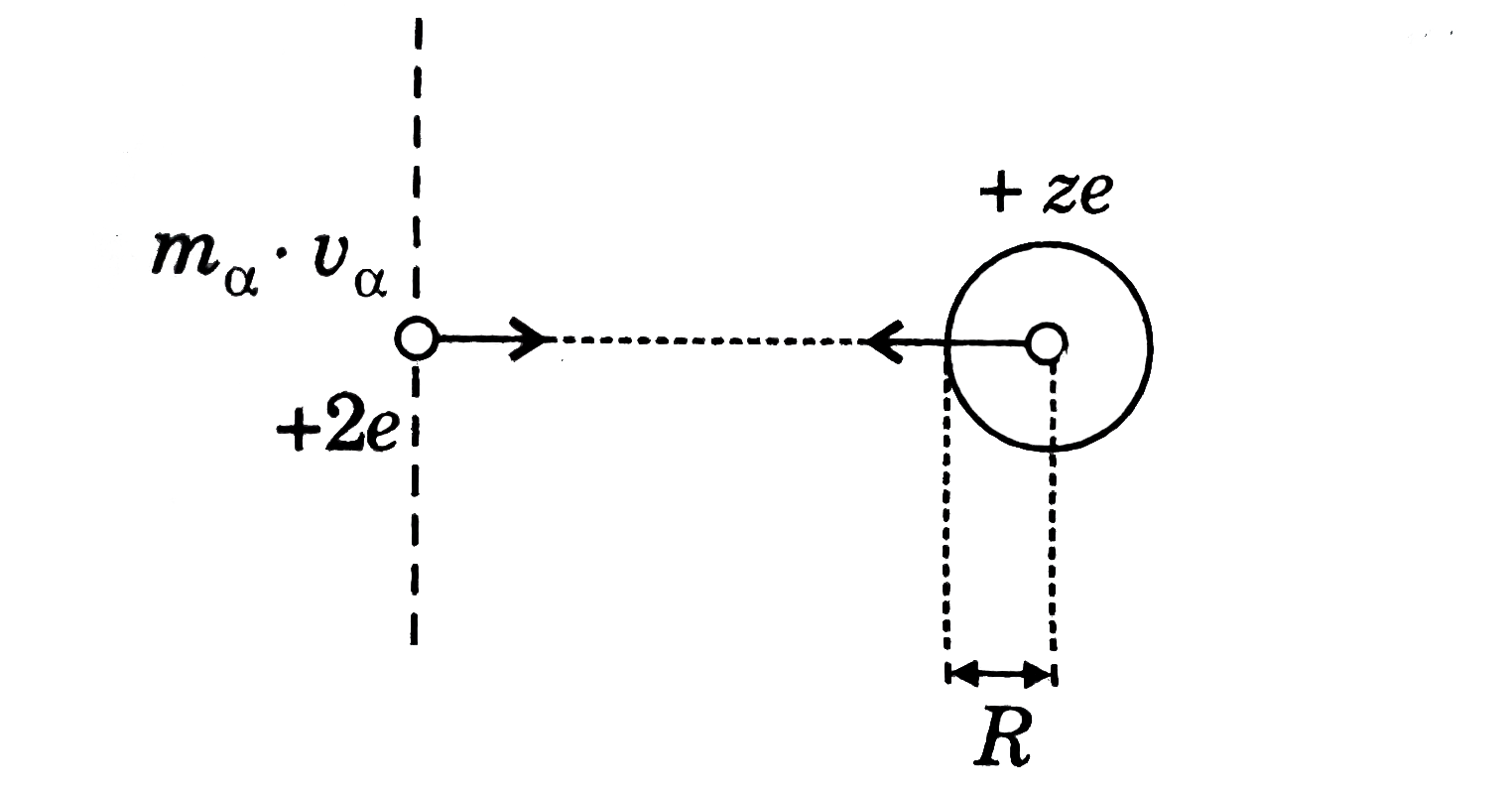
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's $α -$ scattering experiment. If an $α -$ perticle is projected from infinity with speed v, towards the nucleus having z protons then the $a p h a -$ perticle which is reflected back or which is deflected by $180^{\circ}$ must have approach closest to the nucleus. It can be approximated that $α -$ particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
${(Total Energy)}_{initial} = {(Total Enregy)}_{final}$
${(K E)}_{i} + {(P E)}_{i} = {(K E)}_{f} + {(P E)}_{f}$
${(P E)}_{i} = 0, since P E$ of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
$\frac{1}{2} m_{α} v_{α}^{2} + 0 = 0 + \frac{k q_{1} q_{2}}{R}$
$\Rightarrow \frac{1}{2} m_{α} v_{α}^{2} = k \frac{2 e \times z e}{R} \Rightarrow R = \frac{4 k z e^{2}}{m_{α} v_{α}^{2}}$
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
$R = R_{0} {(A)}^{1 / 3}$
where $R_{0} = 1.2 \times 10^{- 15} m$
A= atomic mass number
R=radius of nucleus
If $α -$ particle with speed $v_{0}$ is projected from infinity and it approaches upto $r_{0}$ distance from the nuclei. Then the speed of $α -$ particle which approaches $2 r_{0}$ distance from the nucleus is
A $\sqrt{2} v_{0}$
B $\frac{v_{0}}{\sqrt{2}}$
C $2 v_{0}$
D $\frac{v_{0}}{2}$

RESNICK AND HALLIDAY-THE NUCLEUS-PROBLEMS

Home
Ask Doubt
Profile

Radius of a nucleus is given by the relation R=R0A1/3 where R0=1.3×10−15m and A is mass number. For a nucleon inside a nucleus, de-Broglie wavelength is given by diameter of the nucleus. Average kinetic energy of a nucleon in the Te128 nucleus based on above information will be :

The correct Answer is:3.09×1010K

Topper's Solved these Questions

Similar Questions

Knowledge Check

The radius of a nucleus is given by r0A1/3 where r0=1.3×10−15 m and A is the mass number of the nucleus, the Lead nucleus has A = 206. the electrostatic force between two protons in this nucleus is approximately

If there are N nucleons in a nucleus of radius R, then the number of nucleons in a nucleus of radius 2R will be :

RESNICK AND HALLIDAY-THE NUCLEUS-PROBLEMS

The correct Answer is: $3.09 \times 10^{10} K$

The radius of a nucleus is given by $r_{0} A^{1 / 3}$ where $r_{0} = 1.3 \times 10^{- 15}$ m and A is the mass number of the nucleus, the Lead nucleus has A = 206. the electrostatic force between two protons in this nucleus is approximately