Two plane mirrors are placed parallel to each other at a distance L apart.A point object O placed between them, at a distance L3 from one mirror.Both mirrors form multiple images.The distance between any two images cannot be
3L2
2L3
2L
None of these
The correct Answer is:A
To solve the problem of finding the distance between any two images formed by two parallel mirrors with a point object placed between them, we can follow these steps:
1. Identify the Setup:
- We have two plane mirrors (let's call them M1 and M2) placed parallel to each other at a distance L.
- A point object O is placed between the mirrors at a distance L3 from mirror M1.
2. Calculate the Position of the First Image:
- The first image I1 formed by mirror M1 will be at a distance L3 behind M1. Thus, the position of I1 is:
I1=−L3
3. Calculate the Position of the Second Image:
- The image I1 acts as an object for mirror M2. The distance from I1 to M2 is L+L3=4L3.
- The second image I2 formed by mirror M2 will be at a distance 4L3 behind M2:
I2=L+4L3=7L3
4. Calculate the Position of the Third Image:
- The image I2 acts as an object for mirror M1. The distance from I2 to M1 is L+7L3=10L3.
- The third image I3 formed by mirror M1 will be at:
I3=−(10L3)=−10L3
5. Continue Finding Subsequent Images:
- Continuing this process, we find that the images alternate between the two mirrors, and their positions can be calculated similarly.
6. Calculate Distances Between Images:
- The distances between adjacent images can be calculated:
- Distance between I1 and I2:
d12=I2−I1=7L3−(−L3)=8L3
- Distance between I2 and I3:
d23=I3−I2=−10L3−7L3=−17L3
7. Generalize the Distances:
- The distances between any two adjacent images can be expressed in the form d=2nL3 where n is an integer.
- The possible distances will be multiples of 2L3.
8. Conclusion:
- Since the distances between images are multiples of 2L3, the distance between any two images cannot be 3L2 (as this does not fit the form of 2nL3 for any integer n).
Final Answer:
The distance between any two images cannot be 3L2.
- We have two plane mirrors (let's call them M1 and M2) placed parallel to each other at a distance L.
- A point object O is placed between the mirrors at a distance L3 from mirror M1.
- The first image I1 formed by mirror M1 will be at a distance L3 behind M1. Thus, the position of I1 is:
I1=−L3
- The image I1 acts as an object for mirror M2. The distance from I1 to M2 is L+L3=4L3.
- The second image I2 formed by mirror M2 will be at a distance 4L3 behind M2:
I2=L+4L3=7L3
- The image I2 acts as an object for mirror M1. The distance from I2 to M1 is L+7L3=10L3.
- The third image I3 formed by mirror M1 will be at:
I3=−(10L3)=−10L3
- Continuing this process, we find that the images alternate between the two mirrors, and their positions can be calculated similarly.
- The distances between adjacent images can be calculated:
- Distance between I1 and I2:
d12=I2−I1=7L3−(−L3)=8L3
- Distance between I2 and I3:
d23=I3−I2=−10L3−7L3=−17L3
- The distances between any two adjacent images can be expressed in the form d=2nL3 where n is an integer.
- The possible distances will be multiples of 2L3.
- Since the distances between images are multiples of 2L3, the distance between any two images cannot be 3L2 (as this does not fit the form of 2nL3 for any integer n).
The distance between any two images cannot be 3L2.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (more than one correct choice type)6videos
GEOMETRICAL OPTICS : REFLECTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Linked Comprehension)2videos
GEOMETRICAL OPTICS : REFLECTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PROBLEMS24videos
GEOMETRICAL OPTICS : REFLECTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
Similar Questions
Two plane mirrors are placed parallel to each other. The distance between the mirrors is 10cm. An object is placed between the mirrors at a distance of 4cm from one of them, say M1. What is the distance between the first time formed at M1 and the second image formed at M2 ?
View SolutionTwo plane mirrors X and Y are placed parallel to each other and are separated by a distance of 20 cm. An object is placed between the two mirrors at a distance 5 cm from the mirror X. Find the distance of the first three image formed in the mirror X.
View Solution
Knowledge Check
- Question 1 - Select One
Two plane mirrors are placed parallel to each other at a distance L apart. A point object O placed between them, at a distance L/3 from the mirror. Both mirrors form multiple image. The distance between any two images cannot be
A(a)3L/2B(b)2L/2C(c)2LD(d)None of these - Question 2 - Select One
Two plane mirrors are placed parallel to each other at a distance L apart . A point object O is placed between them, at a distance L/3 from one mirror . Both mirrors form multiple images. The distance between any 'two images cannot be
A3L/2B2L/2C2LDNone of these - Question 3 - Select One
Two plane mirrors are placed parallel to each other at a distance L apart . A point object O is placed between them, at a distance L/3 from one mirror . Both mirrors form multiple images. The distance between any 'two images cannot be
A3L2B2L3C2LDNone of these
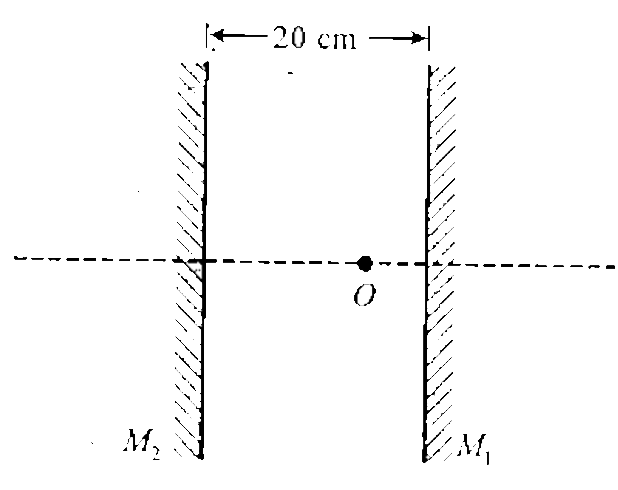
Two plane mirrors M1 and M2 are placed parallel to each other 20 cm apart. A luminous point object 'O' is placed between them at 5 cm from M1 as shown in figure :
 View Solution
View SolutionWhen the two plane mirror are parallel to each other, then the number of images of an object placed between them is
View SolutionTwo plane mirrors parallel to each other and an object O placed between them. Then the distance of the first three images from the mirror M2 will be (in cm) –
 View Solution
View SolutionTwo plane mirrors are inclined at an angle of 72∘ . The number of images of a point object placed between them will be
View SolutionTwo plane mirrors A and B are placed at a distance 12 cm apart facing towards each other . An object is placed in between them at a distance 8 cm from the mirror A . What will be the distance between them at a distance 8 cm from the mirror A . What will be the distance between the first two images formed in the mirror B
View Solution
